Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 182

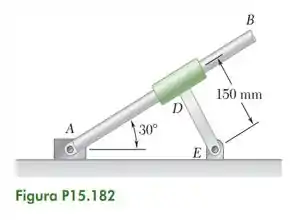
A barra AB passa por meio de um colar que está soldado na ligação DE. Sabendo que no instante mostrado o bloco A se desloca para a direita em uma velocidade constante de 2   m / s , determine (a) a velocidade angular da barra AB, (b) a velocidade relativa ao colar do ponto da barra em contato com o colar, (c) a aceleração do ponto da barra em contato com o colar. (Dica: a barra AB e a ligação DE tem o mesmo ω e o mesmo α .)

Passo 1

O enunciado pede que a gente determine a velocidade angular e a aceleração angular da placa

Pois muito bem! Vamos começar! Do enunciado conseguimos extrair os seguintes dados...

D E = 150   m m

A E = 300   m m

Passo 2

E como a nossa velocidade angular é constante, então temos um movimento rotacional uniforme. De modo que podemos escrever a seguinte equação abaixo...

θ = θ 0 + ω t

Isolando t :

t = θ - θ 0 ω

Como o colar saiu de um ângulo inicial θ 0 = 0 ° = 0   r a d para um ângulo final θ = 90 ° = π 2   r a d , então ficamos com...

t = θ - θ 0 ω

t = π 2 - 0 2 π 3

t = 0,75   s

Que belezinha! O enunciado também nos diz que o colar se movimenta ao longo da barra! Pois muito bem! Esse é um movimento retilíneo uniforme dado pela seguinte equação...

r = r 0 + u t

Se o colar saiu de r 0 = 250   m m para r = 500   m m , num intervalo de tempo de 0,75   s , então somos capazes de obter u ...

u = r - r 0 t

u = 0,5   m - 0,25   m 0,75   s

u = 1 3   m / s

E essa é a velocidade do colar P relativo à barra...

v P / A B = 1 3   m / s   ↑

Passo 3

Continuando nosso raciocínio, chamemos de a P ' a aceleração quando o colar em P coincide com B em r = 500   m m . Esse aceleração vai ser dada por:

a P ' = r ω 2

a P ' = ( 0,5   m ) 2 π 3   r a d / s 2

a P ' = 2 π 2 9   m / s 2   ↓

a P ' ≅ 2,1932     m / s 2   ↓

Passo 4

Quanto à aceleração a P / A B do colar P relativo à barra, esta vai valer zero...

a P / A B = 0

Por fim, calculando a aceleração de Coriolis:

2 ω × v P / A B = 2 ω u = 2 2 π 3 1 3 = 1,3963   m / s 2   ←

Podemos obter a aceleração em S :

a s = a P ' + a P / A B + 2 ω × v P / A B

a s = [ 2,1932     m / s 2   ↓ ] + [ 1,3963   m / s 2   ← ]

a → s = - [ 2,1932     m / s 2 ] j ^ - [ 1,3963   m / s 2 ] i ^

Tirando o módulo e o ângulo de orientação...

a s = - 2,1932 2 + ( - 1,3963 ) 2   m / s 2   tan - 1 ⁡ - 1,3963 - 2,1932

a s = 81,4   r a d / s 2   ⤾

Resposta

No ponto A: a s = 81,4   r a d / s 2   ⤾

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma corrente é enrolada em torno de duas engrenagens de 40m m de raio, que podem girar livremente em relação ao braço A B , de 320m m . A corrente move-se em torno do braço AB no sentido horário a uma
O braço AB tem uma velocidade angular constante de 16 rad / s no sentido anti-horário. No instante em que θ = 90 ∘ , determine a aceleração (a) do colar D, (b) do ponto médio G da barra BD.
O braço AB tem uma velocidade angular constante de 16 rad / s no sentido anti-horário. No instante em que θ = 60 ∘ , determine a aceleração do colar D,
Sabendo que, no instante mostrado, a haste AB tem aceleração angular zero e uma velocidade angular de 15 rad/s no sentido anti-horário, determine (a) a aceleração angular do membro BD, (b) a aceleraçã
A gaiola de um elevador de mina se move para baixo a uma velocidade constante de 40 pés / s. Determine a magnitude e a direção da aceleração de Coriolis da gaiola se o elevador estiver localizado (a)