Exercícios de Movimento Relativo: Aceleração - Lista de Exercícios Resolvida

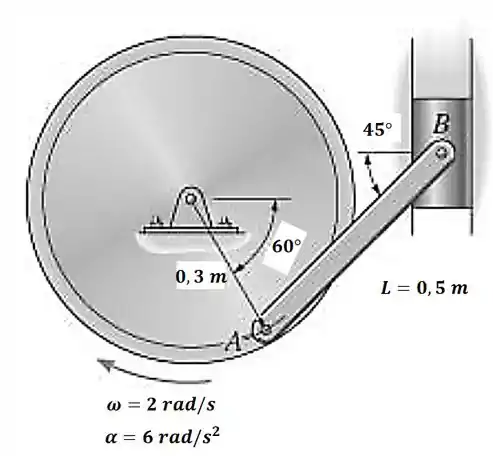
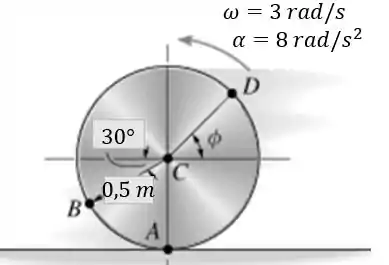
Num dado instante, o volante está girando com a velocidade e a aceleração angulares indicadas na figura. Determine a aceleração do bloco , nesse instante.

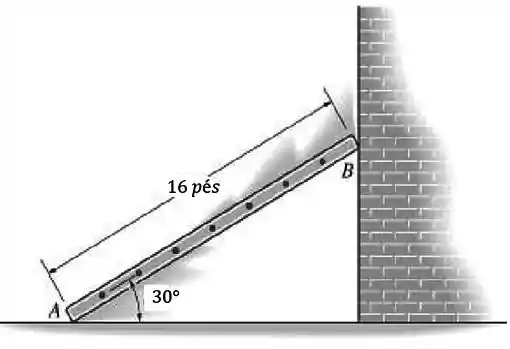
Num dado instante, o pé A da escada tem aceleração e velocidade , ambas para esquerda. Determine a aceleração do topo e a aceleração angular da escada, nesse instante.

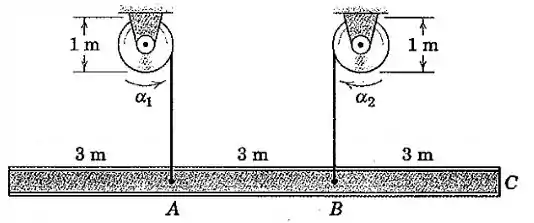
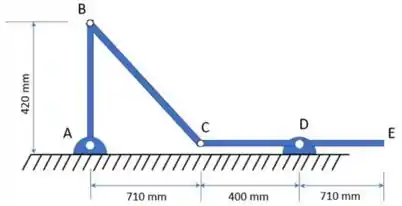
A viga de aço de está sendo levantada a partir de sua posição horizontal pelos dois cabos presos em e . Se as acelerações angulares iniciais dos tambores de elevação são e nos sentidos indicados, determine a aceleração angular correspondente da viga, a aceleração de , e a distância desde até um ponto sobre a linha de centro da viga que não possui aceleração.

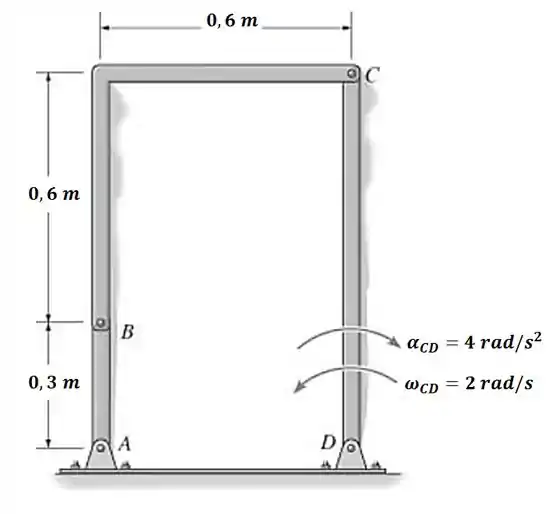
Determine a aceleração angular da barra de ligação , considerando que a barra tem a velocidade e a desaceleração angulares indicadas na figura.

O disco está se deslocando para a esquerda com aceleração angular e a velocidade angular . Se ele não escorrega em , determine a aceleração do ponto .

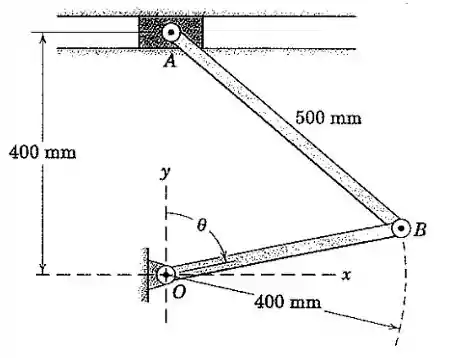
Determine a aceleração angular da barra e a aceleração linear de para se e nessa posição. Desenvolva sua solução usando notação vetorial.

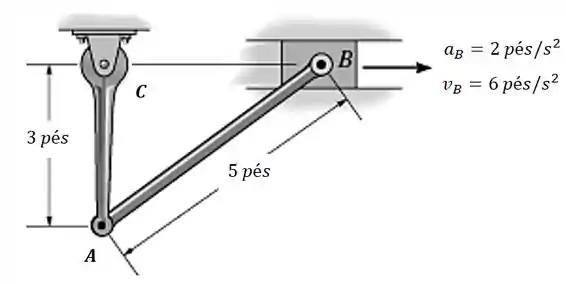
O bloco deslizante move-se para a direita com aceleração de . Na situação mostrada na figura, a velocidade de é de . Determine a aceleração angular da barra e a aceleração do ponto , na situação considerada.

03) As barras , de massa e , de massa , são articuladas entre si no ponto , conforme mostrado na figura. A extremidade da barra é vinculada a uma parede vertical por meio de uma articulação. A extremidade da barra é apoiada em uma superfície horizontal isenta de atrito. Admitindo que as barras se encontrem inicialmente em repouso na configura indicada na figura, pede-se, para o instante em que o sistema inicia o seu movimento:

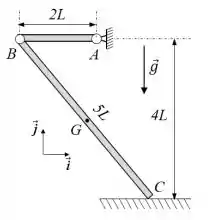
a) Os diagramas de corpo livre das barras e ;

b) a relação entre as acelerações angulares e das barras e , respectivamente;

c) a aceleração do centro de massa da barra em função da aceleração angular ;

d) as acelerações angulares e das barras em função dos parâmetros dados;

e) a reação na extremidade da barra .

Dado:

03) No mecanismo a seguir, no instante mostrado, a barra AB possui velocidade angular de e aceleração angular de , ambas no sentido anti-horário. Nesse instante, a barra BC gira com a mesma velocidade angular da barra AB enquanto a barra CE gira com velocidade angular no sentido horário.

Pede-se:

a) Calcule a aceleração angular da barra BC;

b) Calcule a aceleração do ponto E.

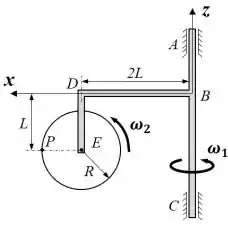
02) A peça gira em torno do eixo vertical com velocidade angular constante , transportando em sua extremidade um disco de raio , o qual, por sua vez, gira com velocidade angular ( constante) em relação à peça . Utilizando o sistema de referência , solidário à peça , e considerando o instante ilustrado na figura, determine:

a) o vetor rotação absoluta do disco;

b) o vetor aceleração rotacional absoluta do disco;

c) as velocidades relativa, de arrastamento e absoluta do ponto do disco.

d) as acelerações relativas, de arrastamento, de Coriolis e absoluta do ponto do disco.

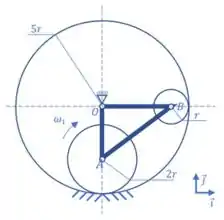
3) A figura ao lado ilustra um mecanismo constituído por um aro fixo de raio e dois discos, um de centro A e raio e outro de centro B e raio , ambos articulados a uma treliça , a qual, por sua vez, é articulada em , centro fixo do aro. O dispositivo assim construído mantém os discos em contato permanente com a superfície interna do aro. Ambos os discos realizam movimento de rolamento sem escorregamento. Sabendo que a velocidade angular do disco de centro A é (constante) e utilizando indicada na figura, pede-se:

a) a velocidade do ponto A.

b) o módulo da velocidade angular do disco de centro B.

c) a velocidade do ponto B.

d) o módulo da velocidade angular da treliça.

e) a aceleração do ponto A.

f) a aceleração do ponto de contato entre o disco de centro A e o aro.

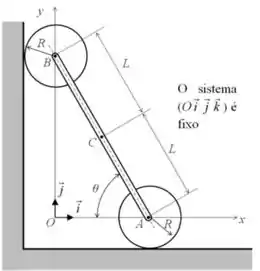
1) Considere o movimento plano da barra AB mostrado no desenho, de comprimento , e articulada sem atrito pelas suas extremidades aos centros de dois discos idênticos de raio R. Os discos mantêm contato com a respectiva superfície e rolam sem escorregar, de modo que o ponto B percorre o eixo e o ponto A percorre o eixo . O referencial fixo é o solo e sabe-se que o vetor de rotação da barra AB é com constante. A partir do instante inicial , quando temos . O sistema de coordenadas é fixo.

São dados: , , .

Para os itens (a) até (e) considere o sistema no instante inicial, quando a barra AB está na vertical .

a) Usando a propriedade fundamental da cinemática do corpo rígido, calcule a velocidade do ponto B.

b) Localize o centro instantâneo de rotação (CIR) do disco de centro A.

c) Localize o CIR da barra AB.

d) Determine o vetor de rotação do disco de centro A.

e) Calcule a aceleração do ponto B da barra AB.

f) No instante em que a barra AB está a , calcule a velocidade do centro C da barra AB, expressando-a no sistema de coordenadas intrínseco.

01) O mecanismo da figura ao lado é composto pelas barras AB e BC de mesmo comprimento , articuladas entre si por meio de um pino B. A extremidade A da barra AB é vinculada a uma articulação fixa e a extremidade C da barra BC é ligada a um pistão que se move ao longo de uma guia vertical. Sabendo que, na configuração ilustrada, a barra AB gira com velocidade angular e aceleração angular , determine:

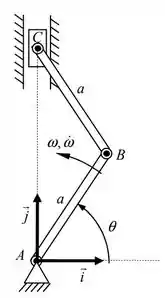
a) a velocidade e a aceleração do ponto B;

b) o centro instantâneo de rotação da barra BC;

c) a velocidade angular da barra BC e a velocidade do ponto C;

d) a aceleração angular da barra BC e a aceleração do ponto C.

3) A figura abaixo representa um dispositivo robótico movendo-se num plano vertical, com aceleração da gravidade . Na extremidade A da coluna fixa há um pequeno motor elétrico que aplica um momento (anti-horário) na extremidade A do braço AB, fazendo este braço girar em torno de A com velocidade angular e aceleração angular , dados. Na extremidade B do braço AB há outro pequeno motor, que aplicar o momento (anti-horário) no braço BC, fazendo-o girar com velocidade angular e aceleração angular A massa do braço AB é , a do braço BC é e ambos podem ser considerados como hastes delgadas homogêneas.

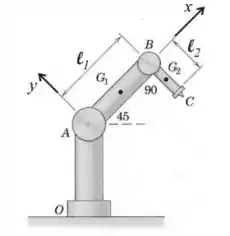
Para a posição indicada na figura, e usando o sistema de eixos indicados, pede-se:

a) Desenhar os diagramas de corpo livre dos braços AB e BC;

b) Escrever as equações do teorema da resultante (TR) e do Teorema da quantidade de movimento angular (TQMA) para o braço BC;

Supondo que o motor em B trave a conexão dos braços AB e BC na posição relativa mostrada, pede-se:

c) obter as expressões de e em função de , das massas e das dimensões dadas na figura;

d) Determinar o momento exercido pelo braço AB sobre o braço BC.

01) Na figura mostrada, temos o ponto P descrevendo uma trajetória circular. Por isso, observe que os movimentos em e estão relacionados.

Se o movimento em é dado por , pede-se, para o instante

a) as velocidades e acelerações do ponto , em coordenadas retangulares;

b) as velocidades e acelerações do ponto em coordenadas ;

c) o raio de curvatura da trajetória de .

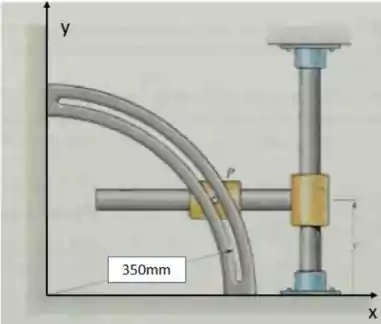
02) Uma barra delgada AB de comprimento gira em torno do eixo vertical com velocidade angular constante . Em sua extremidade B está articulado um disco de raio que gira em torno do eixo perpendicular ao plano da figura com velocidade angular constante . Adotando a base solidária à barra AB, determinar, para a configuração indicada:

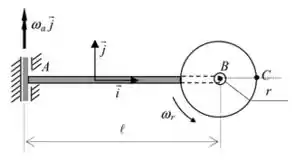
a) O vetor rotação absoluta do disco;

b) O vetor aceleração rotacional absoluta do disco;

c) A velocidade absoluta do ponto C;

d) A aceleração absoluta do ponto C.

1) O mecanismo ilustrado na figura abaixo é constituído por 3 componentes: 1) um suporte ABOD (desenhado em azul) vinculado à articulação A e ao mancal radial B, que gira com velocidade angular constante em torno do eixo vertical; 2) uma luva C (desenhada em verde), que desliza ao longo da haste OD do suporte ABOD com velocidade constante relativa à haste; 3) um disco de raio R, solidário à luva C que gira em torno da haste OD com velocidade angular constante . O sistema de referência móvel é ligado ao suporte ABOD e, no instante mostrado na figura, o ponto P da periferia do disco encontra-se na posição . Nota: Todas as respostas devem ser expressas no sistema de coordenadas .

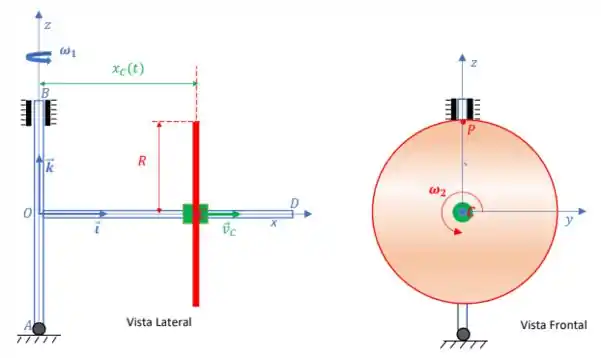
Pedem-se:

a) A velocidade absoluta do ponto C.

b) A aceleração absoluta do ponto C;

c) O vetor rotação absoluta do disco;

d) O vetor aceleração rotacional absoluta do disco;

e) A velocidade absoluta do ponto P;

f) A aceleração absoluta do ponto P.

02) Um disco de massa e raio , articulado pelo seu centro a uma barra AO de massa e comprimento , rola sem escorregar sobre a superfície interna de uma pista fixa em forma de aro circular. O sistema parte do repouso quando a barra está alinhada com a direção horizontal (. A base de versores mostrada na figura é ligada à barra AO.

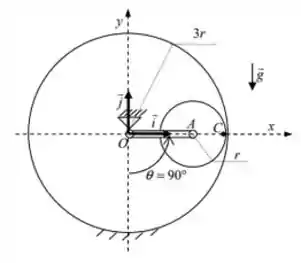
Para um ângulo arbitrário , pede-se:

a) Determinar a relação entre as velocidades angulares do disco e da barra e entre as acelerações angulares do disco e da barra ;

b) Desenhar os diagramas de corpo livre do disco e da barra;

c) Indicar as forças que realizam trabalho nulo, apresentando as devidas justificativas;

d) Escrever a expressão geral da energia cinética do sistema;

e) Determinar a velocidade angular do disco;

f) Determinar a aceleração angular do disco.

03) Um disco homogêneo move-se sobre uma pista plana horizontal sob a ação de uma força passante pelo seu centro de massa. O coeficiente de atrito cinético entre as superfícies do disco e da pista é . Supondo-se que o movimento do disco seja de rolamento sem deslizamento, pede-se:

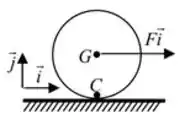
a) Desenhar o diagrama de corpo livre do disco;

b) determinar a aceleração angular do disco e a aceleração do seu centro de massa;

c) determinar as componentes horizontal e vertical da força de contato entre o disco e a pista;

d) estabelecer a condição que deve ser satisfeita para que o movimento hipoteticamente realizado pelo disco – rolamento sem deslizamento – seja possível.

03) O disco homogêneo de centro , raio e massa é articulado em e uma barra homogênea esbelta , de massa , comprimento e inclinada de um ângulo em relação à horizontal, tendo sua outra extremidade ligada a um rolete guiado por uma guia horizontal, conforme ilustrado na figura. Sob a ação de uma força horizontal de módulo constante , o disco rola escorregar sobre um plano horizontal. Desprezando o atrito no contato entre o rolete e a guia horizontal, pede-se:

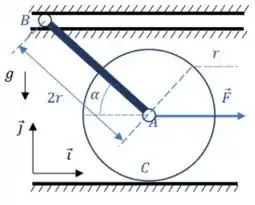
a) A aceleração angular do disco.

b) As magnitudes das componentes da reação em .

c) As magnitudes das componentes da força vincular em .

d) As magnitudes das componentes da reação em .

e) O valor mínimo do coeficiente de atrito entre o disco e a pista para que o disco não escorregue.

02) Um disco de massa , raio e centro , rola sem deslizar sobre um plano inclinado, sendo o ponto de contato. O disco é tracionado por um cabo inextensível, de massa desprezível, ligado por meio de uma polia a um bloco de massa . No instante inicial, o sistema está em repouso e Sabendo que a polia de centro tem massa desprezível, pede-se, para o instante ilustrado na figura:

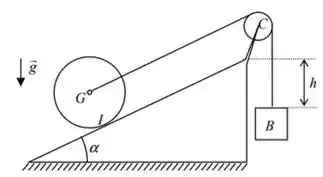
a) a energia cinética do sistema;

b) a velocidade e a aceleração do bloco em função de

c) a tração no cabo e as componentes normal e tangencial da força de contato no disco.

01) A plataforma circular de raio gira em torno do eixo vertical fixo com velocidade angular (constante) e desliza na direção do mesmo eixo com velocidade , conforme mostrado na figura. Uma barra de comprimento é articulada na plataforma em , e gira com velocidade angular (constante) em relação à plataforma. Para a configuração instantânea indicada, e admitindo a plataforma como referencial móvel, calcule e escreve suas respostas nos campos abaixo utilizando o sistema de coordenadas solidário à plataforma.

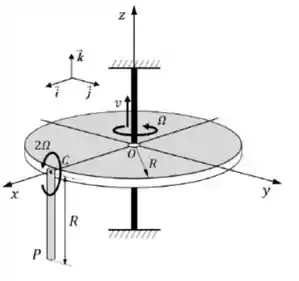
a) As velocidades relativa, de arrastamento e absoluta do ponto da barra.

b) As acelerações relativa, de arrastamento e absoluta do ponto da barra.

c) O vetor rotação absoluta da barra.

d) O vetor aceleração rotacional absoluta da barra.