Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 5.Problemas - Ex. 211
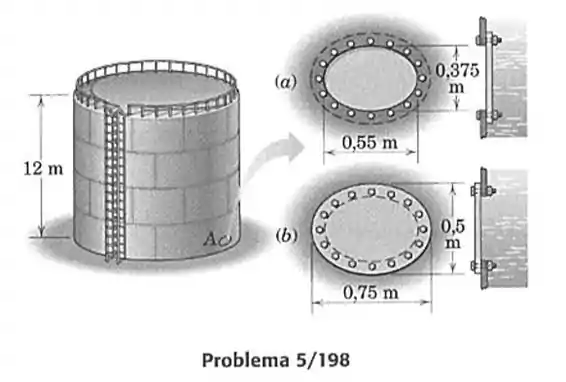
198- A pequena abertura de acesso, , permite que os trabalhadores de manutenção entrem no tanque de armazenamento no nível do chão, quando ele está vazio. Dois projetos, e , estão mostrados para a tampa da abertura. Se o tanque estiver cheio de água doce, estime a pressão média na área de vedação do projeto e o aumento médio na força trativa inicial em cada um dos 16 parafusos do projeto . Você pode considerar a pressão sobre toda a área da abertura como constante e a pressão na área de vedação do projeto pode ser considerada como a atmosférica.
Passo 1
A pressão de água doce a de profundidade pode ser calculada como:
Onde a densidade de água doce é de .
Passo 2
A área de uma elipse é calculada por onde e são os tamanhos dos eixos maior e menor da elipse.
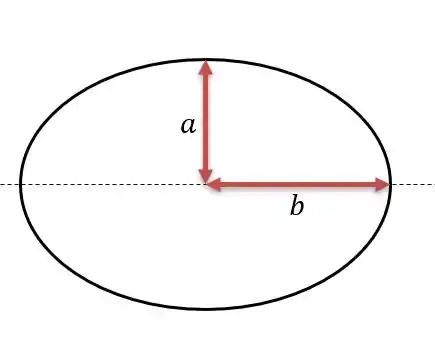
No projeto a área total da porta sofre resiste a carga de água, o que é a área coberta pelos parafusos somada com a que está em contato com a água.
Essa área toda resiste a uma força igual a:
A área para dentro do tanque é calculado como.
Enquanto a área que resiste a pressão é dada por (área onde os parafusos estão) :
Que é a área onde os parafusos estão, que é a região de interesse.
Logo a pressão nos parafusos do projeto é tal que:
Passo 3
Na letra apenas a parte interna da porta suporta a carga de água e não mais toda a porta como na questão anterior, essa alteração faz com que a força resistente de água seja.
Essa força será resistida pelos 16 parafusos, logo: