Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 12
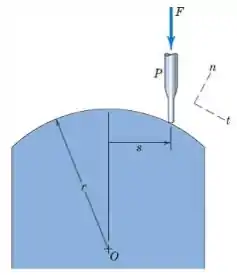
Uma pequena sonda é levemente forçada contra uma superfície circular com uma força , como mostrado. Determine as componentes e desta força como função da posição horizontal .
Passo 1
Olá, tudo bem com você?
O problema pede que determinemos as componentes e da força como função da posição horizontal . Vamos primeiro desenhar para compreender melhor o problema.
Veja que a figura foi feita de uma forma que facilita a visualização. faz um ângulo com o eixo da normal. Temos ali um triângulo retângulo, com hipotenusa e lado menor . Sabemos que, pelo Teorema de Pitágoras, o lado maior corresponde à . Então,
E como
Encontramos a componente normal .
Passo 2
Agora, encontrando a componente tangencial, temos que,
Então,
Encontramos nossa componente tangencial !
Resposta
Exercícios de Livros Relacionados
Um sistema força-binário atua no ponto Oa60 ° do setor circular. Determine o módulo da força F se o sistema dado pode ser substituído por uma força autônoma na extremidade A do setor.
Uma chave de roda é usada para apertar um parafuso de cabeça quadrada. Se forças de 250N forem aplicadas à chave, como mostrado, determine o módulo F das forças iguais exercidas nos quatro pontos de c
Duas hastes e um cabo estão fixados ao suporte em O . Determinar a magnitude F e direção θ da terceira força, caso duas das forças estejam como mostrado, de modo que a resultante das três forças estej
A tensão de 250N é aplicada em um cabo que é envolvido de forma segura em torno da periferia do disco. Determine o sistema força-binário equivalente no ponto C . Comece encontrando o sistema força-bin
A força F atua ao longo da linha M A , em que M é o ponto médio do raio ao longo do eixo x . Determine o sistema força-binário equivalente no ponto O , se θ=40 ° .