Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 7.Problemas - Ex. 60
A suspensão dianteira de eixo duplo é usada em caminhões pequenos. Em um teste do comportamento projetado, o chassi deve ser levantado com um macaco de forma que , para relaxar a compressão nas molas dos amortecedores. Determine o valor de quando o macaco é removido. Cada mola tem uma rigidez de 120 kN/m. A carga vale 12 kN e o chassi central tem uma massa de 40 kg. Cada roda e sua conexão associada tem uma massa de 35 kg com centro de massa a 680 mm da linha de centro vertical.
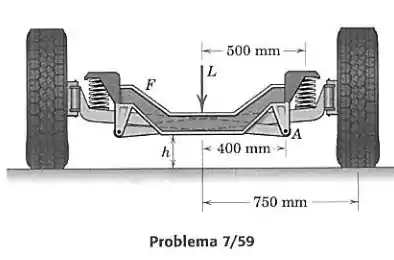
Passo 1
Pelo princípio do trabalho virtual, se o sistema está em equilíbrio e o deslocarmos levantando as rodas de uma altura infinitesimal , o trabalho virtual total realizado pelas forças ativas deve ser igual à variação de energia potencial:
As única forças ativas externas ao sistema (forças que realizam trabalho) são a força normal que o solo aplica nas rodas e o peso das rodas. Vamos considerar o chassi fixo, de modo que a energia potencial gravitacional dessa parte não varie. O movimento da roda da esquerda será em torno do ponto , e o da roda da direita será semelhante. A força potencial é dada pela energia potencial elástica da mola e a energia potencial gravitacional das rodas, e o trabalho virtual é realizado pelas forças do chão. Vamos calcular e para um pequeno aumento da altura da roda, e então igualar.
Passo 2
Primeiro vamos calcular as forças aplicadas pelo solo. Pelo equilíbrio das forças verticais, elas juntas devem ser iguais a soma dos pesos das rodas de massa 35 kg cada, do chassi de 40 kg e da carga de 12 kN:
O trabalho realizado pelas forças para um aumento da altura da roda é então:
Passo 3
Agora vamos calcular a variação da energia potencial gravitacional das rodas. Considerando que o mecanismo gira em torno de , devemos achar a variação da altura das rodas em função de :
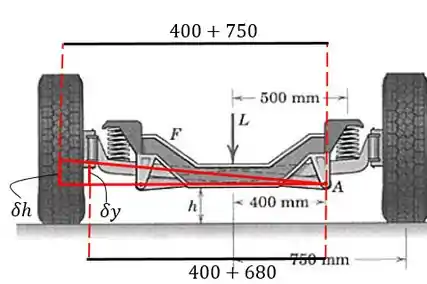
Pela Semelhança de triângulos:
Então a variação da energia potencial das rodas será:
Passo 4
Finalmente, vamos agora calcular a variação da energia potencial da mola. A compressão da mola pode ser calculada semelhante ao modo como fizemos a relação entre e . Como consideramos o ponto fixo e a roda esquerda levantando, após o removimento do macaco a roda se moveu , e então a mola sofreu uma compressão:
Podemos calcular também a adição da compressão da mola em função de :
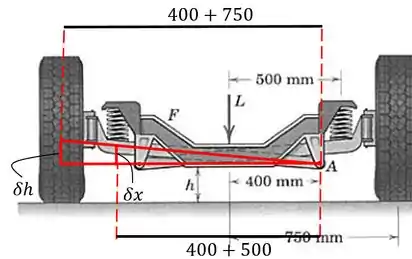
A energia potencial das duas molas juntas é:
Derivando, obtemos o valor da variação infinitesimal da energia potencial elástica:
A constante da mola é igual a :
Substituindo os valores em função de :
Passo 5
Como foi dito no Passo 1, pelo Princípio do Trabalho Virtual a variação da energia potencial deve ser igual ao trabalho:
Então:
Cortando , obtemos o valor de :