199- A prancha de mostrada em seção tem uma massa específica de e bascula em relação ao eixo horizontal através de sua borda superior . Calcule o ângulo assumido pela prancha em relação a horizontal, para o nível de água doce mostrado.
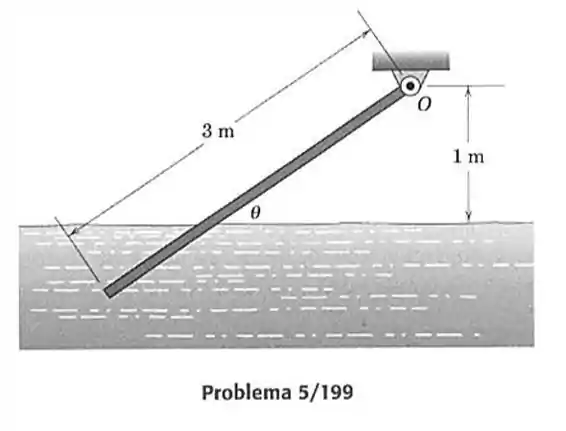
Passo 1
Nesse tipo de questão não estamos muito interessados em saber a força horizontal aplicada na normal da prancha, podemos simplesmente analisar somente com as forças verticais aplicadas na prancha. Isso é a força de reação em , o empuxo e o peso da prancha. Tal como:
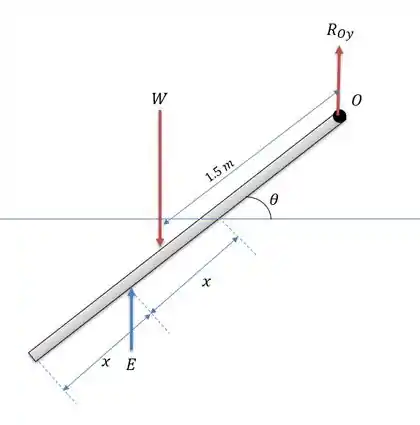
A força pode ser calculado por:
Como não temos como calcular vamos dizer que o volume dessa prancha vale onde é a área da seção transversal e o comprimento total da prancha. O que nos dá:
E o empuxo imposto pelo líquido na prancha.
Onde é toda a superfície da prancha que não está em contato com a água. Que pode ser calculado como:
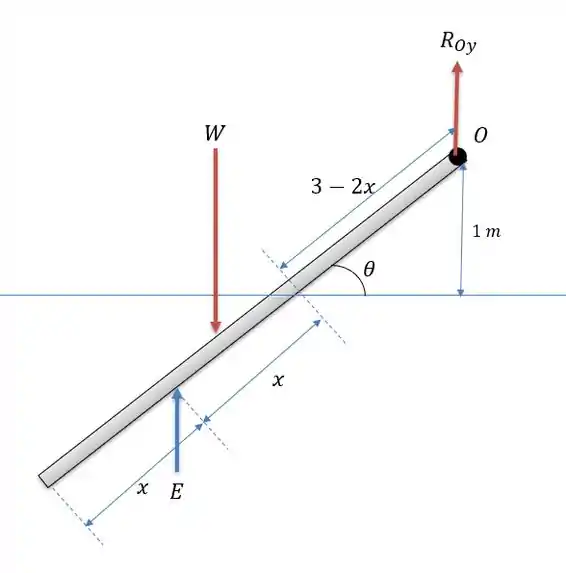
Logo o empuxo pode ser escrito como”
Passo 2
Agora podemos calcular a somatória dos momentos em para encontrar o ângulo . Para isso basta rebater a prancha para baixo para sabermos as distâncias horizontais das forças em .
Substituindo tudo temos: