Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 5.Problemas - Ex. 216
204- A determinação exata da posição vertical do centro de massa de um navio é difícil de ser obtida por cálculo. Ela é mais facilmente obtida por um experimento simples de inclinação do navio carregado. Fazendo referência á figura, uma massa externa conhecida, . É colocada a uma distância da linha de centro e o ângulo de adernagem é medido por meio da deflexão de um prumo de chumbo. O deslocamento do navio e a posição do metacentro são conhecidos. Calcule a altura do metacentro para um navio de , inclinado devido a uma massa de colocada a da linha de centro, se um prumo de chumbo com de comprimento é defletido de uma distância . A massa está a uma distância acima de . [Observe que a tonelada métrica é igual a e equivale ao megagrama (Mg) ]
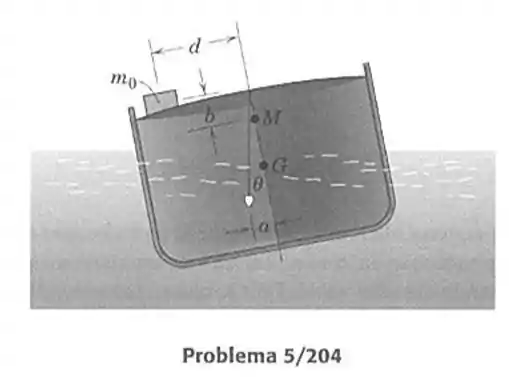
Passo 1
Além do sistema de forças precisamos traçar muito bem a geometria do problema, uma vez que precisaremos determinar o ângulo para poder achar a distância que o problema quer.
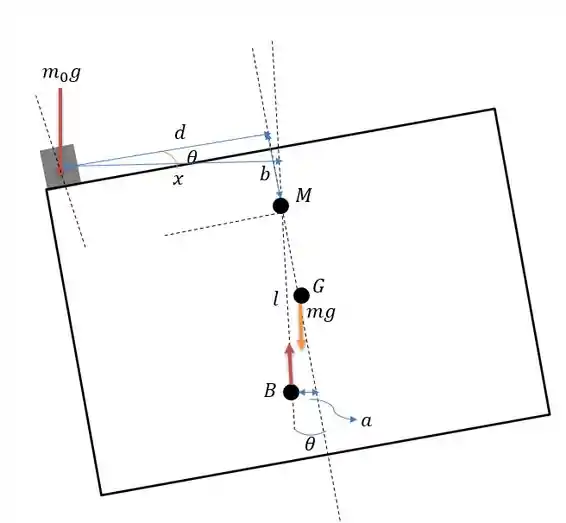
Inicialmente podemos calcular pelo deslocamento do prumo de chumbo que nos dará um triângulo retângulo tal que:
Onde a é a deflexão horizontal do mesmo e que foi dado, que valerá e o comprimento total que vale , logo:
Passo 2
Com esse ângulo vamos dar um zoom na figura e conseguir tirar as medidas que queremos:
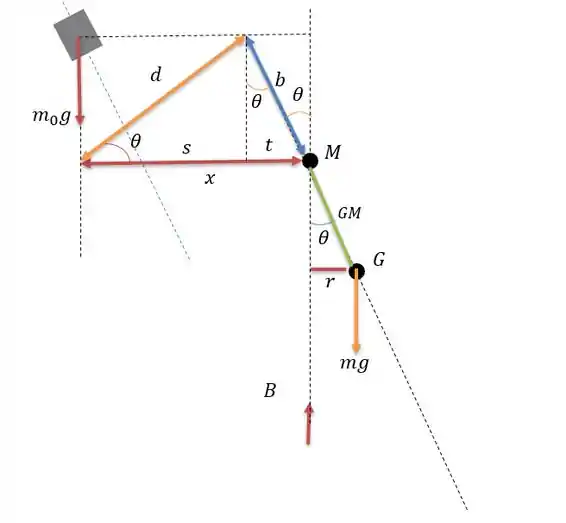
Se fizermos a somatória dos momentos em temos a seguinte expressão:
Onde se tira do triângulo formado pela hipotenusa que nos dá:
E pela soma de e tal que:
Logo
Como e temos:
Passo 3
Substituindo os resultados na relação do momento temos com e :