Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 2.Problemas - Ex. 11
2.12. O dispositivo é usado para a substituição cirúrgica da articulação do joelho. Se a força que atua ao longo da perna é , determine suas componentes ao longo dos eixos e .
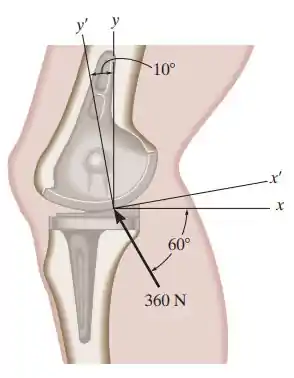
Passo 1
Fala galera boa, bora resolver essa parada sem enrolação?
Aqui a gente precisa encontrar as componentes em x e y’ da força, na nossa língua significa usar a regra do paralelogramo mas antes vamos aos desenhos dos vetores.
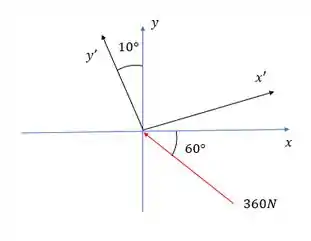
Agora vamos fazer o seguinte, precisamos usar a regra do paralelogramo pra ver onde estão as forças Fx e Fy’, pra isso bora prolongar a força F até o segundo quadrante e desenharemos o paralelogramo.
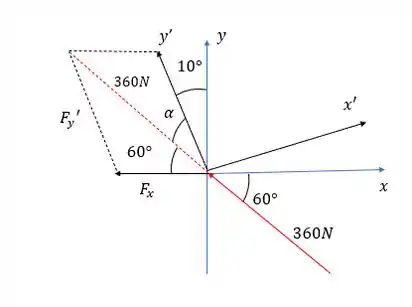
Repare que o ângulo entre e é , então
Daqui podemos extrair o seguinte triângulo
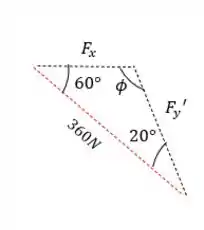
Agora podemos descobrir o ângulo do triângulo usando a propriedade que diz que a soma dos ângulos internos de um triângulo é 180°, então
Passo 2
Agora só precisamos usar a lei dos senos para determinar a intensidade das forças. Vamos começar por
O sinal negativo ali no existe porque está no sentido oposto a .
Passo 3
Agora a gente usa a mesma estratégia para calcular