Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 31

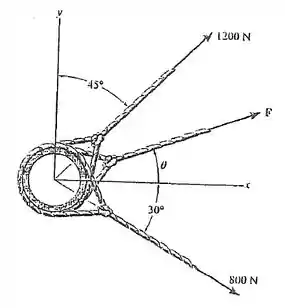
2.31. Três cabos puxam um tubo de tal modo que geram uma força resultante com intensidade de 1800   N . Se dois dos cabos estiverem submetidos a forças conhecidas, como mostra a figura, determine o ângulo θ do terceiro cabo, de modo que a intensidade da força F neste cabo seja mínima. Todas as forças estão localizadas no plano x-y. Qual é a intensidade de F? Dica: Determine a resultante das duas forças conhecidas.

Passo 1

Fala, querido. Aqui ele quer duas coisas. Ele quer a orientação de F (o ângulo θ ) e quer também o valor dela.

Mas o fofo já dá um bizu: Ele fala para calcularmos a resultante das forças conhecidas. E por que? Cara, para F ser mínima, ela precisa estar na direção da força resultante entre elas.

Agora pensa comigo. Se F está na resultante das forças conhecidas, a resultante das três forças juntas vai estar em que direção?

Só pensar, a resultante das 3 forças é a resultante das duas forças conhecidas (que atua na direção de F ) mais a força F . Temos então duas forças somadas na mesma direção. A resultante dessas duas forças fica na mesma direção! O que nos diz que 1 8 00   N está na direção de F .

Então, vamos seguir o bizu do enunciado e achar a orientação de F R 1 , que é θ e depois achamos F .

Passo 2

Vamos começar calculando F R 1 que é a resultante de F 1 = 1200   N   e   F 2 = 800 , como a dica do exercício diz.

F R 1 → = F 1 → + F → 2

Vamos fazer um esqueminha dessa soma vetorial:

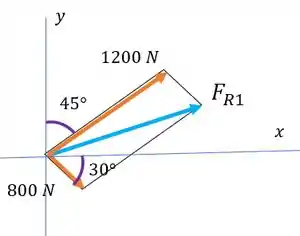
Percebe que a gente montou um paralelogramo. Os lados paralelos dele são iguais, então a gente pode extrair daí esse triângulo:

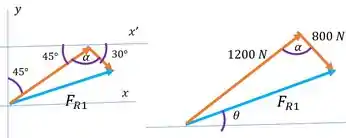
Daí. Pela figura da esquerda, a gente pode achar esse ângulo α assim:

180 ° = 45 ° + α + 30 ° → α = 105 °    

Pela lei dos cossenos, tiramos que:

F R = 1200 2 + 800 2 - 2 ⋅ 1200 ⋅ 800 ⋅ cos ⁡ 105 °  

F R = 1605,28   N

Passo 3

Podemos extrair o outro triângulo que forma o paralelogramo, assim:

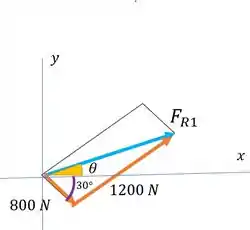
Percebe que a gente posicionou nosso θ . Se a gente chamar ϕ = θ + 30 ° e lembrar que o ângulo entre as forças laranjas é 105 °

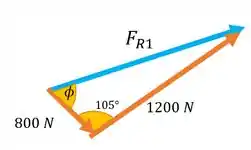
Daqui podemos tirar pela lei dos senos que

sin ⁡ ϕ 1200 = F R 1

sin ⁡ ϕ 1200 = sin ⁡ 105 ° 1605,28

Então

ϕ = s i n - 1 1200 ⋅ sin ⁡ 105 ° 1605,28 = 46,22 °

Então

ϕ = θ + 30 °

θ = 46,22 ° - 30 ° = 16,2 °

Passo 4

Agora podemos calcular a intensidade mínima para F. Lembra que F e 1 8 00   N tinham a mesma direção? Então podemos escrever:

F R = F R 1 + F 1 8 00 = 1605,28   + F F = 194,72   N

Resposta

F = 194,72   N θ = 16,2 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tanque de aço deve ser posicionado em uma escavação. Sabendo-se que α = 20 ° , determine, usando a trigonometria, (a) a intensidade requerida para a força P se a resultante R das duas forças aplica
Um carrinho de mão que se movimenta ao longo da viga horizontal é acionado por duas forças indicadas na figura. (a) Sabendo-se que α = 25 ° , determine, usando trigonometria, a intensidade da força P
Resolva o problema 2.3 usando trigonometria.
Dois elementos estruturais A e B são parafusados a um suporte, como mostra a figura. Sabendo que ambos os elementos estão em compressão e que a força é 15k N no elemento A e 10k N no elementro B . Det
Para o suporte tipo gancho do Problema 2.1, usando trigonometria e sabendo que a intensidade de P é 75N , determine (a) a intensidade requerida da força Q se a resultante R das duas forças aplicadas e