Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 88
Determine a distância entre as extremidades e do arame definindo primeiro um vetor posição de a e depois determinando sua intensidade.
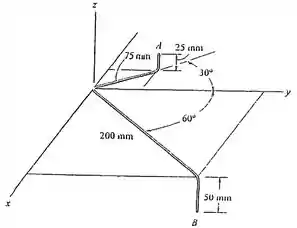
Passo 1
A distância que o exercício nos pede é o módulo do vetor entre os pontos e , então vamos começar encontrando as coordenadas dos pontos.
Para , já temos a altura em , nosso está no sentido negativo do eixo e nossa informação é dada através do ângulo com o eixo , então:
Para também já temos a altura em enquanto e são positivos:
Definimos agora nosso vetor posição pelo ponto final menos inicial com seus devidos vetores unitários, assim:
E finalmente podemos descobrir a distância através do módulo do nosso vetor:
Resposta
Exercícios de Livros Relacionados
2.28. A viga deve ser içada usando-se duas correntes. Determine as intensidades das forças F AeF B que atuam em cada corrente, a fim de obter uma força resultante de 600N orientada ao longo do eixo y
2.26. A tora deve ser rebocada por dois tratores A e B. Determine as intensidades das duas forças de reboque F A e F B , levando-se em conta que a força resultante tenha uma intensidade F R = 10 k N e
2.25. Duas forças F 1eF 2 atuem sobre o gancho. Se suas linhas de ação formam um ângulo θ e a intensidade de cada força é F 1 = F 2 = F , determine a intensidade da força resultante F R e o ângulo ent
Determine o vetor posição r direcionado do ponto A ao ponto B e o comprimento da corda A B . Considere z = 4m .
Se a corda A B possui 7,5m de comprimento, determine a posição da coordenada + z do ponto B .