Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 22
2.22. Se , e a força resultante deve ser orientada ao longo do eixo y positivo, determine a intensidade da força resultante, se necessita ser mínima. Além disso, quais valores de e do ângulo ?
Passo 1
Fala ai galerinha, xuxu beleza?
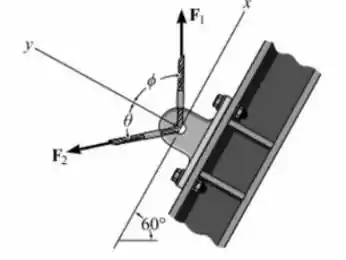
Saca só, nesse exercício aqui o enunciado nos disse que duas forças e atuam sobre um suporte como dado na figura abaixo:
Ele nos dá que a força possui módulo e ângulo e pede pra gente encontrar a força mínima tal que a resultante fique na mesma direção do eixo , ou seja, na verdade queremos uma força tal que:
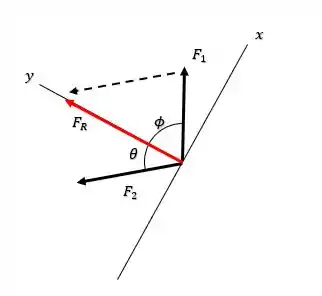
Agora que vem a primeira malandragem, porque se a gente analisar os ângulos possíveis entre e o eixo de atuação com a força , veremos que:
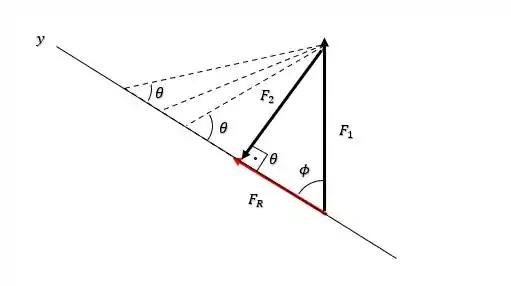
Quando o ângulo é igual a , o tamanho de necessário para a resultante permanecer no eixo é o menor possível, ou seja, será mínimo quando ângulo entre ela e o eixo for igual a .
Passo 2
Iradoso, agora que descobrimos que a perpendicular ao eixo , podemos encontrar seu módulo.
Como a resultante está no eixo , quer dizer que a soma das forças no eixo deve ser igual a , tal que:
Sendo assim:
Passo 3
Belezinha então, agora pra gente encontrar o valor da força resultante podemos usar as relações do triângulo formado por e .
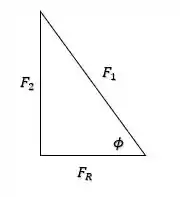
Como temos um triangulo retângulo, podemos aplicar o Teorema de Pitágoras, tal que:
Logo:
Portanto: