Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 60

60. Determine a velocidade do ponto A na borda da engrenagem no instante mostrado.

Passo 1

Um esboço que pode ajudar na resolução do problema pode ser representado por:

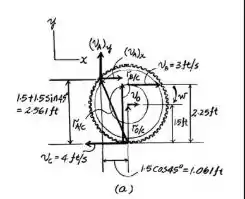
Passo 2

Aplicando a equação de velocidade relativa entre os pontos B e C, vem que:

v B = v C + ω × r B / C

0,9 i = - 1,2 i + - ω k × 0,675 j

0,9 i = 0,675 ω - 1,2 i

A partir daí:

0,9 = 0,675 ω - 1,2

ω = 3,111   r a d / s

Passo 3

Para o ponto A e C,

v O = v C + ω × r A / C

( v A ) x i + ( v A ) y j = - 1,2 i + ( - 3,111 k ) × ( - 0,323 i + 0,780 j )

( v A ) x i + ( v A ) y j = 1,2089 i + 1,0057 j

Logo,

( v A ) x = 1,2089   m / s

( v A ) y = 1,0057   m / s

A intensidade da velocidade em A, é dada por:

v A = v A x 2 + v A y 2 = 1,57   m / s

e a orientação é dada por:

θ = tan - 1 ⁡ ( 1,0057 / 1,2089 = 39,8 °

Resposta

v A = 1,57   m / s

θ = 39,8 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

15.49. No sistema de engrenagens planetárias mostrado na figura, o raio da engrenagem central A é a, o raio das engrenagens planetárias é b e o raio da engrenagem externa E é a +-2b. A velocidade angu
15.51. O braço AB gira com uma velocidade angular de 20 rad /s no sentido anti-horário. Sabendo que a engrenagem C é estacionária, determine (a) a velocidade angular da engrenagem B, (b) a velocidade
15.51. O braço AB gira a uma velocidade angular de 42 rpm no sentido horário. Determine a velocidade angular requerida da engrenagem A para que (a) a velocidade angular da engrenagem B seja de 20 rpm
15.50. A engrenagem A gira com uma velocidade angular de 120 rpm no sentido horário. Sabendo que a velocidade angular do braço AB é 90 rpm no sentido horário, determine a velocidade angular correspond
15.54. O braço ACB gira em torno do ponto C com velocidade angular de 40 rad /s no sentido anti-horário. Dois discos de atrito A e B estão presos por pinos em seus centros ao braço ACB do modo mostrad