Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 54

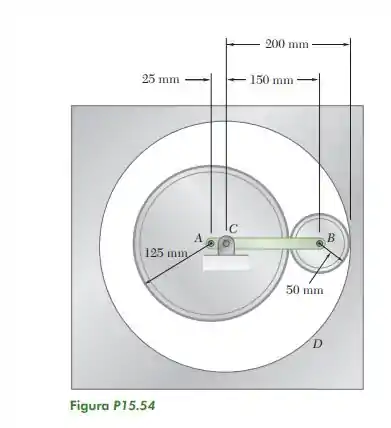
15.54. O braço ACB gira em torno do ponto C com velocidade angular de 40 rad /s no sentido anti-horário. Dois discos de atrito A e B estão presos por pinos em seus centros ao braço ACB do modo mostrado na figura. Sabendo que os discos rolam sem escorregar nas superfícies de contato, determine a velocidade angular (a) do disco A, (b) do disco B.

Passo 1

Bom, nós podemos começar o exercício calculando as velocidades no ponto A e no ponto B, a gente consegue fazer isso já que o enunciado nos da a velocidade angular no ponto C.

v A = r A C ⋅ ω C

Isso fica

v A = 25 ⋅ 40 = 1 000 m m s

E

v B = r B C ⋅ ω C

Isso fica

v B = 150 ⋅ 40 = 6 000 m m s

Então temos

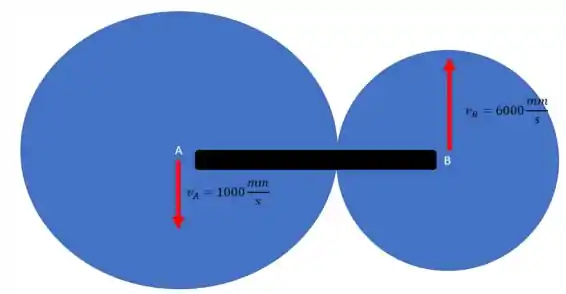
Passo 2

Agora vamos começar a resolver.

Repare na figura, a translação e rotação do disco B terão a mesma velocidade, pois uma a translação causa a rotação, veja, conforme o disco B translada por conta do Braço ABC ele tem um contato com D, esse contato que faz ele rotacionar, então

v B = v B '

Sendo v B ' a velocidade de rotação. Logo

v B = r B ⋅ ω B

Então

ω B = v B r B = 6000 50 = 120 r a d s

Passo 3

Vamos usar um raciocínio parecido para o disco A. Bom, o disco A tem o movimento de translação, de rotação e o movimento por conta do contato com o disco B. A velocidade da borda do disco B é a mesma velocidade da borda do disco A, vamos chamar essa velocidade de v ' .

Bom, para calcular a velocidade na borda do disco B que está em contato com A podemos fazer:

v ' = v B + v B '

Ou também

v ' = v A + v A '

Então

v A + v A ' = v B + v B '

Logo

v A + r A ⋅ ω A = v B + r B ⋅ ω B

Vamos isolar ω A

ω A = v B + r B ⋅ ω B - v A r A

Substituindo os valores

ω A = 6000 + 50 ⋅ 120 - 1000 125 = 88   r a d s

Resposta

a : ω A = 88 r a d s b : ω B = 120 r a d s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um mecanismo para empurrar pequenas caixas de uma linha de montagem para uma correia transportadora é mostrado com o braço OD e a manivela CB em suas posições verticais. A manivela gira no sentido hor
No instante representado, a = 150 mm e b = 125 m, e a distancia a + b entre A e C está diminuindo na taxa de 0,2 m/s. Determine a velocidade em comum V dos pontos B e D para esse instante.
O mecanismo é parte de um dispositivo de engate onde a rotação do elemento AOB é controlada pela rotação do elemento ranhurado D em torno de C. Se o membro D possui uma velocidade angular no sentido h
Os elementos do mecanismo para a implantação da lança do magnetômetro de uma nave espacial são mostrados. Determine a velocidade angular da lança quando o elemento de acionamento OB ultrapassa o eixo
A roda rola sem deslizar. Para o instante representado, quando O está diretamente sob o ponto C, a barra AO possui uma velocidade V = 1,5m/s para a direita e θ = 30 ° . Determine a velocidade angular