Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 52

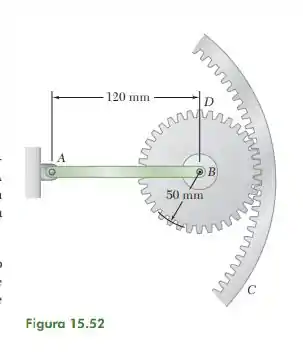
15.51. O braço AB gira com uma velocidade angular de 20 rad /s no sentido anti-horário. Sabendo que a engrenagem C é estacionária, determine (a) a velocidade angular da engrenagem B, (b) a velocidade do dente da engrenagem no ponto D.

Passo 1

Podemos começar essa questão aqui calculando a velocidade no ponto B. Sabendo que o braço AB tem uma velocidade angular de 20 r a d s , podemos fazer

v B = r A B ⋅ ω A B  

Que fica

v B = 120 ⋅ 20 = 2400 m m s

Passo 2

Bom, outra maneira que poderíamos calcular a velocidade de B é

v B = r B ⋅ ω B

Veja, a velocidade em C é estacionaria, então o ponto B muda de posição conforme a engrenagem gira, ou seja, a velocidade do ponto B depende só da velocidade angular da engrenagem B.

Logo

ω B = v B r B

ω B = 2400 50 = 48 r a d s

Essa é a resposta do item (a).

Passo 3

Agora vamos para o item (b). Uma possível maneira de calcularmos é

v D ' = v E ' + v D E

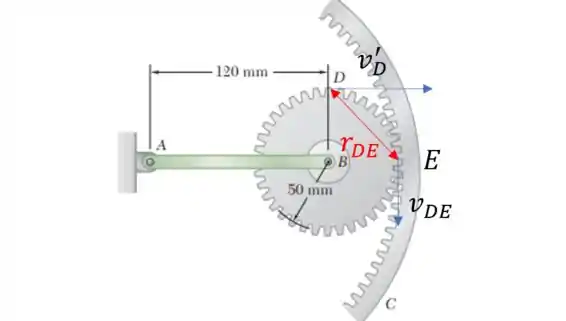
Sendo v E ' a velocidade do dente na engrenagem e v D E a velocidade relativa entre o dente de D e o dente de E. Essa velocidade pode ser calculada assim:

v D E = r D E ⋅ ω B

E a velocidade de E é nula, pois a engrenagem C está em repouso.

v E ' = 0

Então

v D ' = r D E ⋅ ω B

Repare na imagem que r D E pode ser considera a hipotenusa do triangulo que tem os dois catetos iguais a 50   m m , então

r D E = 2 ⋅ 50 2 = 70,71   m m

Portanto]

v D ' = 70,71 ⋅ 48 = 3394 m m s

Ou no SI

v D ' = 3,39 m s

Resposta

a : ω B = 48 r a d s b : v D ' = 3,39 m s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5/114) O cilindro pequeno rola sobre asuperfície do cilindro grande sem deslizar . Utilizando o centro instantâneo de velocidade nula do cilindro pequeno , determine a velocidade v A do ponto A indica
5/111) Os elementos do mecanismo para a implantação da lança do magnetômetro de uma nave espacial são reapresentados aqui a partir do Prob.5/87 . Pelo método dessa seção , determine a velocidade angul
5/116) A engrenagem D (os dentes não são mostrados) gira no sentido horário em torno de O com uma velocidade angular constante de 4r a d / s . O setor de 90 °A O B está montado sobre um eixo independe
5/117) O projeto do mecanismo mostrado , o cursor A deve deslizar ao longo do eixo fixo conform o ângulo θ aumenta . Quando θ = 30 ° , o elemento de controle em D deve ter uma componente de velocidade
5/119) O movimento do rolete A contra sua mola restritiva é controlado pelo movimento descendente do êmbolo E . Para um intervalo de movimento a velocidade de E é v = 0,2m / s . Determine a velocidade