Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 63
63.O carro sustenta o engradado uniforme com massa de . Determine as reações verticais sobre os roletes em e . O rolete em não é mostrado. Despreze massa do carro.
Passo 1
Primeiro temos que avaliar que tipos de conexões temos nessa situação, nesse caso são roletes e segundo a tabela do capítulo , seção , esse tipo de conexão só exerce uma força vertical para cima.
Temos que saber também qual a força exercida pelo engradado sobre o carrinho, mas isso é fácil, já que essa força vai ser igual a força peso da caixa que é dada por:
Onde é a massa do objeto e é a aceleração da gravidade. Logo a força peso do carrinho é:
Considerado a massa do engradado uniforme, podemos assumir que essa força se concentra no centro do engradado.
Abaixo temos o diagrama de corpo livre da situação.
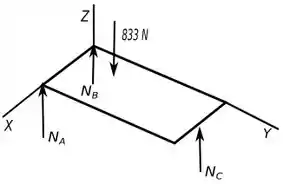
Agora para determinar e vamos usar as equações de equilíbrio.
Passo 2
Vamos primeiro usar a equação de equilíbrio referente ao momento em relação ao eixo , pois envolve apenas uma variável o , já que as outras duas não contribuem para o momento.
Passo 3
Agora vamos usar a seguinte equação de equilíbrio:
Passo 4
Agora só falta achar e vamos fazer isso através da equação de equilíbrio da força na direção .