Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.5 - Ex. 69

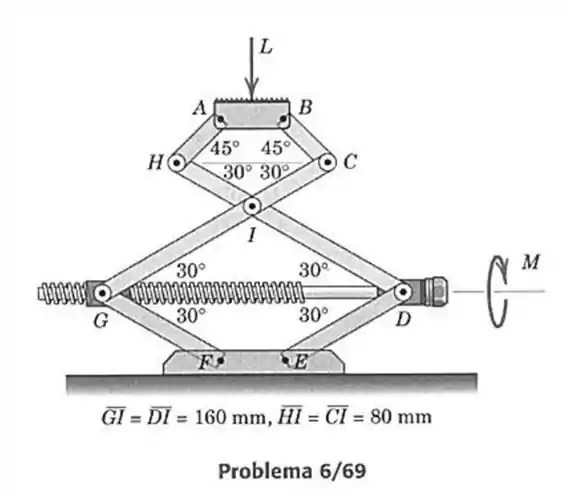
69- Um macaco sanfona com uma rosca quadrada única, que rosqueia na bucha e gira em um mancal de rolamentos em , está sendo projetado. A rosca deve ter um diâmetro de e um passo (avanço por revolução) de . Com um coeficiente de atrito para as roscas engraxadas, calcule o torque no parafuso necessário para levantar uma carga de desde a posição mostrada e calcule o torque necessário para abaixar a carga a partir da mesma posição. Considere que a plataforma e a linha permanecerão horizontais sob a carga. Despreze o atrito no mancal em .

Passo 1

Para resolver esse problema nós precisamos encontrar a força axial que surge no eixo . Para isso vamos tratar esse macaco como uma treliça, e a primeira abordagem que temos que ter ao resolver treliças é primeiro calcular a reação nos seus apoios.

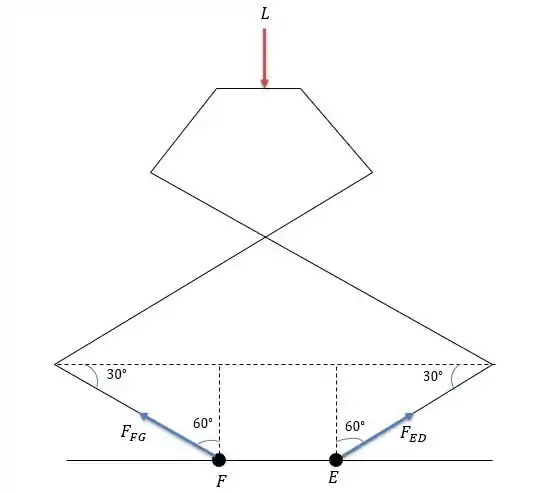
E os dois apoios estão representados na figura acima, e pela simetria da geometria do macaco podemos dizer que:

Projetando essas duas forças na vertical nós teremos:

Passo 2

Agora podemos começar decompor nossas forças nos elementos da barra. Vamos começar pela somatória das forças no corpo .

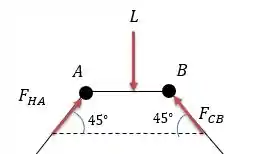
Pela simetria e pela somatória das forças horizontais encontramos que:

Agora pela somatória das forças verticais temos que:

Passo 3

Agora podemos calcular a força axial no parafuso ao se utilizar da figura abaixo.

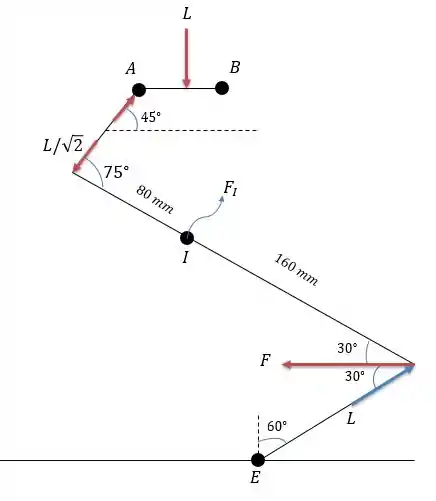
Note que se fizermos o cosseno de com o ângulo de essa força estará paralela a barra, o que não é bom para calcularmos o momento, para garantir que ela estará perpendicular devemos utilizar o seno.