Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 70
Determine a força compressiva em cada uma das três pernas do tripé submetido à força vertical de . O peso das pernas é desprezível comparado à carga aplicada. Resolva usando a equação de equilíbrio de forças .
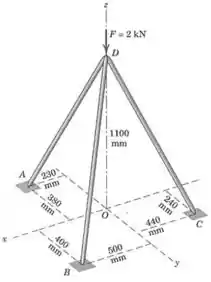
Passo 1
Precisamos escrever todas as forças na forma vetorial. Para isso precisamos encontrar os vetore unitários na direção de cada perna:
E agora para encontrar a forma vetorial das forças só precisamos multiplicar os vetores unitários pelos módulos correspondentes.
E a força de pode ser escrita da seguinte forma:
Passo 2
Agora, aproveitando a sugestão do enunciado, vamos usar a condição de equilíbrio:
E quando somamos essas quatro forças, e consideramos que todas as componentes têm que se anular, ficamos com um sistema de três equações:
E agora temos que resolver esse sistema para encontrar , e .
Passo 3
A melhor forma de resolver essa sistema é escrevendo na forma matricial:
E você pode usar qualquer um dos vários métodos que existem para resolver um sistema como esse. Como esse não é um curso de álgebra matricial, pode resolver usando uma calculadora.
Nesse caso temos:
E esses são os módulos das forças (todos em Newtons). E todas são compreessivas (em nenhum caso apareceu um sinal negativo).
Resposta
As forças compressivas são , e .