Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 86
86. Determine os componentes das reações em e quando a estrutura é carregada por um binário no sentido horário de intensidade de aplicado em em .
Passo 1
Tudo nesse problema vai ser resolvido na base das equações de equilíbrio (novidade kkk).
Então teremos que analisar as seguintes equações:
Em relação aos pontos ou direções que forem mais convenientes.
Os apoios que temos em e em , mostrados na figura, vão nos fornecer forças na direção e .
Só para ficarmos bem orientados vamos adotar o sentido positivo do momento o anti-horário.
Passo 2
Começando com aplicação do momento em , vamos começar analisando a equação do momento, tanto faz se em relação a ou em , a diferença é qual componente das reações desses pontos vamos descobrir primeiro.
Então escolhendo analisar a equação do momento em relação ao ponto .
Passo 3
Agora como temos o podemos analisar a equação de equilíbrio da força na direção , pois assim fica fácil de achar , então:
Vamos analisar agora na direção , para ver o temos:
Eita, temos um problema, não sabemos nenhuma das duas incógnitas, mas vamos ver umas coisas que nos podem ajudar.
Passo 4
Vamos lá, vamos usar um truque usando proporcionalidade em triangulo retângulo envolvendo as intensidades das forças e o comprimento dos lados do triangulo, olhe a seguinte figura abaixo só do membro .
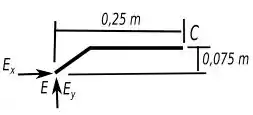
Assim podemos ver o seguinte:
Sendo que , logo:
Tendo podemos achar pela última equação do passo .
Passo 5
Agora vamos fazer a aplicação do momento em , vamos começar analisando a equação do momento, tanto faz se em relação a ou em , a diferença é qual componente das reações desses pontos vamos descobrir primeiro.
Então também escolhendo analisar a equação do momento em relação ao ponto .
Passo 6
Agora como temos o podemos analisar a equação de equilíbrio da força na direção , pois assim fica fácil de achar , então:
Vamos analisar agora na direção , para ver o temos:
Eita, temos o mesmo problema de novo, não sabemos nenhuma das duas incógnitas, vamos usar a mesmo truque que usamos anteriormente.
Passo 7
Vamos lá, vamos usar o truque usando proporcionalidade em triangulo retângulo envolvendo as intensidades das forças e o comprimento dos lados do triangulo, olhe a seguinte figura abaixo só do membro .
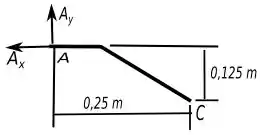
Assim podemos ver o seguinte:
Sendo que , logo:
Tendo podemos achar pela última equação do passo .