Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 93
93. Dois tudo de de diâmetro (tubo 1 e tubo 2) são sustentados a cada por uma pequena estrutura tal como a mostrada na figura. Sabendo que o peso de cada tubo somado ao seu conteúdo é e considerando superfícies sem atrito, determine os componentes das reações em e .
Passo 1
Primeiro, temos que saber o peso de cada tubo e para isso vamos usar a informação do enunciado que diz que o peso desse tubo está distribuído em , sendo que está apoiado por um sistema parecido com o da figura a uma distância de , então temos que:
Para esse problema temos que usar as equações de equilíbrio, mas para isso precisamos achar as distancias entre os pontos, já que para calcular momento isso é necessário.
Precisaremos também achar as forças de contato entre os tubos e os apoios, só que como os tubos são iguais se acharmos para um, acharemos para o outro. Vamos fazer isso usando trigonometria e avaliando o diagrama de corpo livre de um dos tubos.
Um detalhe a se notar é que por simetria temos a seguinte igualdade , agora só falta descobrir o valor kkkk.
Passo 2
Vamos analisar o diagrama de corpo livre do tubo para acharmos o valor das forças de contato em e .
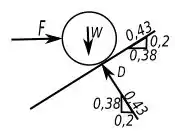
A relação de proporcionalidade que está exposta no “chão” onde o tubo está apoiado vem da própria figura fornecida pelo enunciado e as medidas presentes nela e se você reparar a força em também apresenta quase a mesma proporção pelo fato dessa ser perpendicular a superfície de apoio do tubo.
Disso podemos tirar a seguinte geometria:
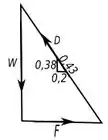
Disso podemos tirar que:
E que:
Passo 3
Agora vamos achar os valores de , pois assim achamos de todos os outros como foi dito no passo . Para isso vamos olhar a figura abaixo.
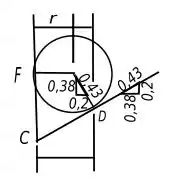
Pela relação de proporcionalidade presente na figura, temos que:
Mas o valor de já sabemos, vale , então:
Consequentemente temos:
Passo 4
Agora podemos partir para análise da equação de momento, mas para isso vamos tomar apenas o membro da montagem e as forças de reação que agem nesse membro. Analisando a equação de momento em relação ao ponto , temos:
Passo 5
Agora como foi mencionando no passo as forças de contato entre os suportes es os tubos são as mesmas tanto para quanto para , logo:
Com isso, podemos analisar a equação de equilibro referente ao momento em relação ao ponto , então temos:
Logo:
Passo 6
Agora, só falta achar as reações em e vamos fazer isso, usando as equações de equilíbrio referente a força nas direções e .
Agora para :