Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 122
122- A força de é aplicada a alavanca da prensa em . Sabendo que , determine a força vertical exercida no bloco em , a força exercida no elemento em .
Passo 1
Analisando as forças em e pelo diagrama de corpo todo nós temos:
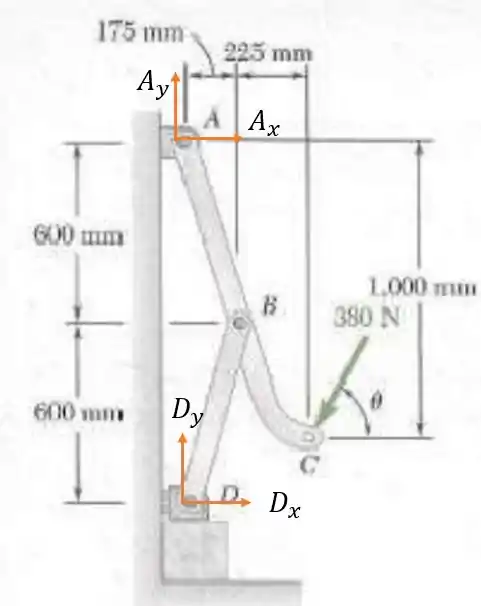
Fazendo a somatória dos momentos em temos:
Dessa forma pela somatória das forças horizontais:
E pela somatória das forças verticais nós temos:
Passo 2
Agora vamos analisar a barra .
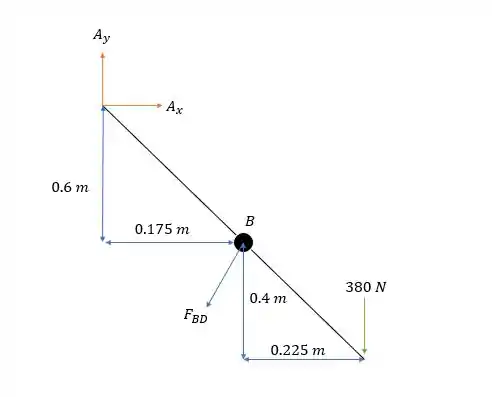
Sabendo que as forças ativas não mudam de direção, vamos calcular a somatória dos momentos em .
Dessa forma o valor de pela equação do passo é:
O que nos dá um módulo igual a:
Que faz um ângulo com a horizontal igual a:
Que se você olhar bem, faz sentido com o ângulo do triângulo retângulo a qual ela pertence.
Passo 3
O valor de sendo aplicada em é o módulo que encontramos de , porém com o ângulo inverso (pela ação e reação) ou seja: