Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 76
Determine a força exercida no elemento e a componente da reação em .
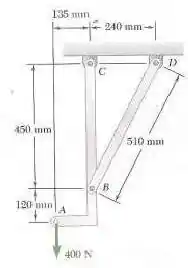
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Quando tratamos as treliças, temos apenas forças em direção de compressão ou tração em uma determinada barra. Mas, nos casos de máquinas e/ou estruturas rígidas, podem atuar várias forças e em direções desconhecidas.
Para a solução desses problemas, vamos encontrar as forças externas desconhecidas, de modo a fazer o diagrama de corpo livre da estrutura e calcular as reações.
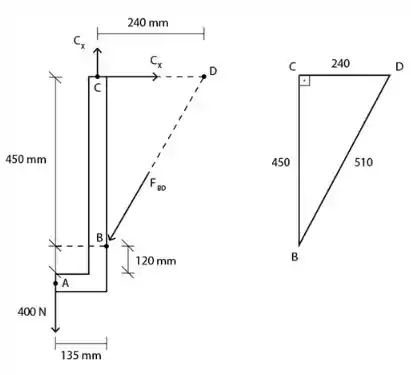
Passo 2
Vamos fazer o somatório dos momentos no ponto :
Passo 3
Fazendo somatório das forças na horizontal, temos:
Fazendo somatório das forças na vertical, temos:
Resposta
Exercícios de Livros Relacionados
Determine a força no elemento A C da treliça carregada. Os dois elementos com formato de ¼ de círculo atuam como elementos de duas forças.
Cada elemento da treliça é uma barra uniforme de 8 m pesando 400 kg. Calcule a tração ou compressão média em cada elemento, devida aos pesos dos elementos.
A treliça é formada por triângulos de lado a e está carregada e apoiada como mostrado. Determine as forças nos elementos E F , D E e D F .
Determine as forças nos elementos B C e B G da treliça carregada.
Uma ponte levadiça está sendo levantada por um cabo E I . As quatro cargas mostradas nos nós são devidas ao peso do pavimento. Determine as forças nos elementos E F , D E , D F , C D e F G .