A água doce do pântano é drenada para o oceano através de uma comporta automática de de largura e de altura. A comporta é mantida por articulações localizadas ao longo da aresta superior em e anteparos na soleira em . Se o nivel da água no pântano é , determine o nível do oceano para que a comporta possa ser aberta. (O peso específico da água salgada é ).
Passo 1
Bom galera, a gente vai começar fazendo um diagraminha de corpo livre, pra nortear a gente:
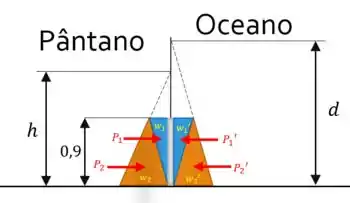
Passo 2
Vamos lá, como o a comporta tem uma largura de , a gente tem que:
Então, calculando os pesos:
Passo 3
Bom, com o que a gente já descobriu, a gente pode deduzir que:
E também:
Passo 4
Agora, vamos analisar o momento, adotando como eixo de rotação e usando a equação de equilíbrio:
Substituindo e desenvolvente, chegaremos em:
Agora, com e :
E já temos esses valores que o problema deu, então: