Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 147

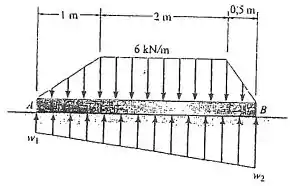
Determine as intensidades w 1 e w 2 do carregamento distribuído agindo na parte inferior da plataforma, de modo que esse carregamento tenha uma força resultante equivalente que seja igual mas oposta à resultante do carregamento distribuído atuando no topo da plataforma.

Passo 1

A fim de determinar a força resultante de ambos os lados, a intensidade equivale à soma de todas as forças que estão atuando em cada carga distribuída. Por esse fato, a resultante que seria definida pela integração entre uma força por unidade de comprimento e um elemento de comprimento, ela pode ser determinada pela área abaixo da curva da carga distribuída, ou seja:

F R = ∫ L w x d x = ∫ A d A = A

E a sua posição de atuação em relação a um ponto de referência pode ser determinada através do princípio dos momentos, já que são relacionadas as forças envolvidas e a distância delas até o ponto de referência para os momentos ocorrerem.

Passo 2

Para a parte superior e inferior, existem forças distribuídas que são trapezoidais e que podem ser divididas em outras áreas mais simples tal como retângulos e triângulos. Então, a força resultante será dada pela soma dessas áreas e deve ser nula para que as resultantes em ambos os lados sejam iguais:

↑ F R = F R i n f e r i o r - F R s u p e r i o r

F R = 0 = A r e t i n f e r i o r + A t r i a n g i n f e r i o r - A t r i a n g 1 , s u p e r i o r - A r e t 1 , s u p e r i o r - A t r i a n g 2 , s u p e r i o r

F R = 0 = ( w 1 ) 3,5 + 1 2 w 2 - w 1 3,5 - 1 2 6 1 - 6 2 - 1 2 6 0,5

Logo,

1,75 w 1 + 1,75 w 2 = 3 + 12 + 1,5

w 1 + w 2 = 16,5 1,75   ( 1 )

Passo 3

Da mesma forma que a força resultante é igual em ambas as partes superior e inferior, é evidente que o momento resultante em cada uma delas deve ter o mesmo valor.

Lembrando que a distância para calcular o momento gerado por uma força distribuída é dada pela posição do centroide da área sob essa força até o ponto de referência, deve-se lembrar também que a posição do centroide de um triângulo é calculada como:

x ¯ t r i a n g = b 3

Deve-se atentar que a posição do centroide do triângulo retângulo é medido a partir do cateto vertical, ou seja:

E do centroide de um retângulo é:

x ¯ r e t = b 2

Passo 4

Logo, aplicando o princípio dos momentos em relação ao ponto A , admitindo que o momento é positivo no sentido horário, tem-se que:

M R A = 0 = F R d

0 = ( w 1 ) 3,5 x ¯ r e t i n f e r i o r + 1 2 w 2 - w 1 3,5 3,5 - x ¯ t r i a n g i n f e r i o r -

- 1 2 6 1 1 - x ¯ t r i a n g 1 , s u p e r i o r - 6 2 1 + x ¯ r e t s u p e r i o r -

- 1 2 6 0,5 3 + x ¯ t r i a n g 2 , s u p e r i o r

Substituindo os valores das posições dos centroides:

0 = ( w 1 ) 3,5 3,5 2 + 1 2 w 2 - w 1 3,5 3,5 - 3,5 3 - 1 2 6 1 1 - 1 3 - 6 2 1 + 2 2 -

- 1 2 6 0,5 3 + 0,5 3

2,0417 w 1 + 4,0833 w 2 = 30 , 75   ( 2 )  

Passo 5

Logo, com as equações (1) e (2) pode-se obter a solução delas que serão os valores desejados:

w 1 = 3,79 6   k N / m

w 2 = 5 , 633   k N / m

Resposta

w 1 = 3,79 6   k N / m

w 2 = 5 , 633   k N / m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o comprimento b da carga triangular e sua posição a sobre a viga, de modo que a força resultante equivalente seja zero e o momento de binário resultante seja 8 kN  m em sentido horário.
Se o solo exerce uma distribuição trapezoidal de carga sobre o fundo do alicerce, determine as intensidades w1 e w2 dessa distribuição, necessárias para suportar as cargas das colunas.
Substitua este carregamento por uma força resultante equivalente e especifique sua posição, medida a partir do ponto O.
Uma forma é usada para moldar um muro de concreto com largura de 5 m. Determine a força resultante equivalente que o concreto molhado exerce sobre a forma AB se a distribuição de pressão do concreto p
Substitua o carregamento por uma força resultante e um momento de binário equivalentes no ponto A.