Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 77
Determine (a) a carga distribuída na extremidade da viga tal que a reação em seja nula, (b) as reações correspondentes em .
Passo 1
Bom galera, a gente vai calculando a força resultante da carga na viga, que é a área que é um trapézio:
Passo 2
Show de bola, o centroide a gente pode encontrar no final do livro, para isso vamos dividir em duas figuras, assim:
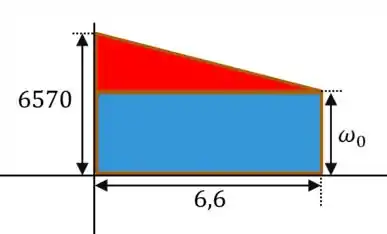
Montamos então, uma tabela para encontrar o centroide :
E por definição temos que o centroide é dado por:
Passo 3
Agora, nós vamos usar a equação de equilíbrio do momento para encontrar as reações, vamos considerar o eixo de rotação porque é onde temos um momento atuando:
Lembra que a gente vai considerar .
Assim a gente encontra:
E a gente também monta outra equação porque sabemos que:
Passo 4
Por fim, nós podemos montar um sisteminha simples, bem assim:
Por substituição, temos:
Resolvendo, encontramos:
Agora, substituindo esse valor em , fica assim: