Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 33
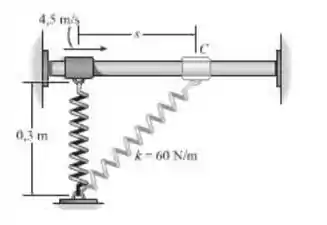
O anel C de 1 kg ajusta-se livremente no eixo liso. Se a mola está livre quando e ao anel é dada uma velocidade de , determine a velocidade do anel quando .
Passo 1
Temos um problema que envolve molas! Portanto, vamos relembrar antes como calculamos a força de uma mola. Dada uma mola de constante elástica e deformada por um comprimento , a sua força é:
Para podermos calcular a força da mola, precisamos descobrir antes quem é este comprimento . Ao olharem a figura da questão vocês podem ver um triângulo retângulo (catetos 0,3 e s). Portanto, o valor será a diferença do valor desta hipotenusa com o comprimento inicial da mola!!! Legal, né!!
Feito isto, podemos partir para a parte do diagrama livre e por fim, finalizaremos na análise de cinemática para podermos resolver a questão.
Passo 2
Antes de fazermos o esboço do diagrama de corpo livre, vamos calcular esta deformação da mola, seguindo o procedimento do passo 1. Portanto, temos:
Agora sim, podemos partir para o diagrama de corpo livre. Desta forma, temos:
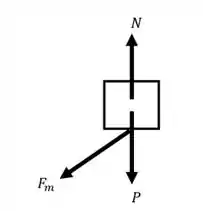
Sendo assim, ao fazermos o somatório ao longo do eixo , obteremos:
Passo 3
Agora, precisamos resolver a equação do Passo 2. Nela, temos a aceleração como função da posição . Para resolvermos, basta lembrarmos que . Resolvendo esta EDO, obteremos o valor da aceleração e chegaremos ao fim da nossa questão!! Vamos as nossas contas então: