Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 47
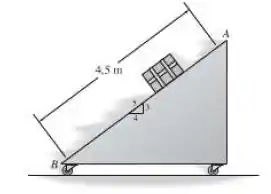
A rampa de rolagem livre tem massa de . A caixa, cuja massa é , desliza, partindo do repouso em , rampa abaixo até . Determine a velocidade da rampa quando a caixa atingir . Suponha que a rampa é lisa, e despreze a massa das rodas.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Aplicando conservação de energia:
Aplicando conservação de quantidade de movimento, temos:
Substituindo os valores, temos:
Analisando o movimento relativo, temos:
Em :
Em :
Relacionando as queações encontramos:
Como temos a componente em e em , podemos relacionar com a magnitude da velocidade :
Relacionando com a equação da conservação de energia, temos:
Resposta
Exercícios de Livros Relacionados
O piloto de um avião a jato avariado foi capaz de controlar seu avião reduzindo a potência dos motres. Se o avião tem uma massa de 8500 kg e um raio de giração k G = 1,41 m em relação ao centro de mas
A montagem de barras lisas mostrada está em repouso quando é golpeada por um martelo em A com um impulso de 10 N.s. Determine a velocidade angular do conjunto e a intensidade da velocidade de seu cent
A montagem tem uma massa de 5 kg e raio de giração k G = 0,18 m em relação a seu centro de massa G. A energia cinética da montagem é 46,5 N.m quando ela está na posição mostrada. Se ela rola no sentid
Se o boxeador bate no saco de pancada de 75 kg com um impulso I = 20 N.s, determine a velocidade angular do saco imediatamente após ele ser atingido. Determine também a localização d do ponto B, em to
O volante de 100 kg tem um raio de giração em relação a seu centro de gravidade O de k O = 0,225m , Se ele gira no sentido anti-horário com uma velocidade angular de 1200 rev/min antes de o freio ser