Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 33
O avião a jato possui uma massa de e um arrasto (resistência do ar) de a uma velocidade de em uma determinada altitude. O avião consome ar na taxa de através de sua abertura de admissão e usa combustível na taxa de . Se a descarga tem uma velocidade para trás de em relação ao bocal de escape, determine o ângulo máximo de elevação em que o jato pode voar com uma velocidade constante de na altitude específica em questão.
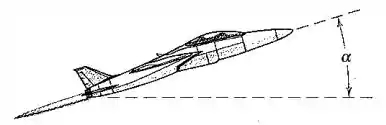
Passo 1
Para que o avião suba com velocidade constante, as forças na direção de subida devem se equilibrar, então:
onde é a força devida ao escoamento, é a componente do peso nessa direção e é o arrasto. Já temos:
Passo 2
Para calcular , faremos assim:
Podemos então substituir todas as forças na equação de equilíbrio:
Resposta
Exercícios de Livros Relacionados
As três esferas idênticas, cada uma de massa m , estão apoiadas no plano vertical sobre o plano inclinado de 30 ° . As esferas estão soldadas às duas hastes de conexão de massa desprezível. A haste su
A extremidade superior da corrente de elos de comprimento L e massa ρ por unidade de comprimento é liberada a partir do repouso com a extremidade inferior quase tocando a plataforma da balança. Determ
No teste estático do conjunto de um motor a jato e um bocal de exaustão, o ar é sugado para o motor na taxa de 30k g / s e o combustível é quimado na taxa de 1,6k g / s . A área de escoamento, a press
Uma rigidez de k = 200 N / m e não está deformando quando o bloco de 25k g está em A . Determine a aceleração do bloco quando s = 0,4m . A superfície de contato entre obloco e o plano é lisa.
Se o motor M exerce uma forca F = 10 t 2 + 100 N sobre o cabo, onde t é dado em segundos, determine a velocidade da caixa de 25k g quando t = 4s . Os coeficientes de atrito estático e cinético entre a