Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas - Ex. 20

O anel tem massa de 0,5   k g e está apoiado sobre a superfície da mesa. Em um esforço para mover o anel, o dedo exerce uma força P sobre ele. Se essa força for direcionada para o centro O do anel, conforme mostra a figura, determine sua intensidade quando o anel estiver em iminência de deslizamento em A. O coeficiente de atrito estático em A é u A   =   0,2 e, em B, u B   =   0,3 .

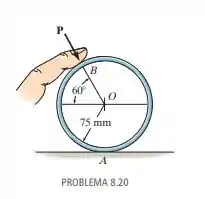
Passo 1

Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão.

Primeiramente, vamos determinar a força de atrito que não permite o deslizamento. Sabemos que:

F a t = F N u = 0,5 × 10 × 0,2 = 1   N

Agora, vamos determinar a resultante normal da força P   para que possamos calcular a força de atrito que força o anel a girar. Logo:

F a t 2 = P u

No entanto, queremos a sua componente tangencial, que gira o anel:

F a t 2 = P s e n 60 u

Para a iminência de deslizamento:

F a t = F a t 2

1 = P s e n 60 × 0,3

P = 3,84   N

Prontinho, esta é a força pedida.

Resposta

P = 3,84   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A argola uniforme de peso W está suspensa pelo pino em A e uma força horizontal P é lentamente aplicada em B. Se a argola começa a deslizar em A quando o ângulo é θ = 30 ° , determine o coeficiente de
A bobina com massa de 150k g se apoia sobre o piso em A e contra a parede em B. Determine a força P necessária para iniciar o desenrolar do fio horizontal para fora da bobina. O coeficiente de atrito
O disco de 45k g se apoia sobre a superfície para a qual o coeficiente de atrito estático é u=0,2 . Determine o maior momento de binário M que pode ser aplicado à haste sem causar movimento.
O dispositivo de travamento por atrito é fixado por um pino em A e se apoia contra a roda em B. Ele permite a liberdade de movimento quando a roda está girando em sentido anti-horário em relação a C.
O disco de 45k g se apoia sobre a superfície para a qual o coeficiente de atrito estático é u=0,15 . Se M=50N m , determine a força de atrito em A .