O dispositivo de travamento por atrito é fixado por um pino em A e se apoia contra a roda em B. Ele permite a liberdade de movimento quando a roda está girando em sentido anti-horário em relação a C. A rotação no sentido horário é impedida pelo atrito da trava, que tende a prender a roda. Se , determine o ângulo de projeto que impedirá o movimento no sentido horário para qualquer valor do momento aplicado M. Dica: desconsidere o peso do trinco, de modo que ele se torna um membro de duas forças.
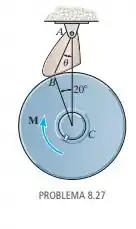
Passo 1
Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão.
O primeiro passo é determinar a força que é gerada pelo momento, da forma:
Esta força é tangencial ao círculo no ponto Logo, devemos decompor esta força em normal e tangencial:
Com a normal, podemos obter o atrito, da forma:
Igualando à força tangencial: