Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 40
Assumindo que a viga prismática tem uma seção transversal retangular, mostrar que para o carregamento dado, o máximo valor da densidade de energia de deformação específica da viga é
onde é a energia de deformação da viga e é seu volume.
Passo 1
Oier, pessoal! Tudo suave? Bora resolver um exercício de energia de deformação para dominar melhor essa matéria?
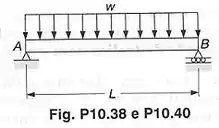
O enunciado quer que a gente prove que a densidade de energia máxima de uma viga da figura abaixo e a energia de deformação dessa viga se relacionem de acordo com a equação que está na figura.
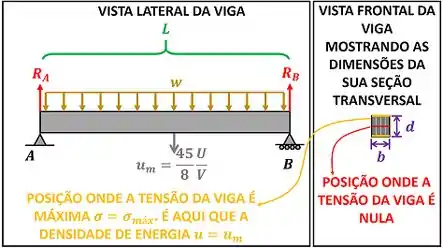
é a largura da viga e é a altura da seção transversal da viga. e são as forças de reação nos pontos e respectivamente.
Pela figura, nós notamos que a viga atinge sua tensão máxima nas extremidades superior e inferior da viga. Por isso, é nessa região que a densidade de energia é máxima .
Provar que e se relacionam de acordo com a equação da figura é a mesma coisa que provar que a divisão entre e vale
Por isso, vamos calcular e e vamos dividir os dois para demonstar que a equação acima é verdadeira.
Calculamos a partir da equação abaixo.
onde é a máxima tensão normal que existe em uma viga sob flexão e é o módulo de elasticidade da viga.
Para calcular a energia da barra causada pelo momento fletor é:
onde é o comprimento total da barra , é o módulo de elasticidade e é o momento de inércia.
Agora que sabemos disso tudo, vamos partir pra resolução do exercício.
Passo 2
Vamos começar a resolver o exercício, calculando o valor de da viga. Nós já sabemos que a máxima densidade de energia ocorre nas extremidades da barra. No entanto, para calculá-la precisamos descobrir quanto vale a tensão nesse ponto. A equação de se encontra na figura abaixo.
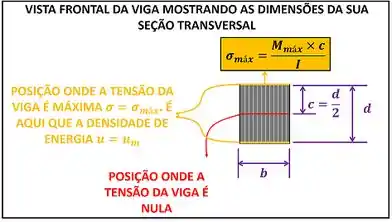
é a distância entre as extremidades da viga e a linha central de tensão nula. Essa distâncaa vale . é o momento fletor máximo da vida. Para saber onde ocorre o ponto de máximo momento fletor , precisamos usar a equação de equilíbrio de momento da parte esquerda da barra no ponto . No entanto, para usar a equação de momento no ponto , precisamos achar o valor de através da equação de equilíbrio de momento no ponto .
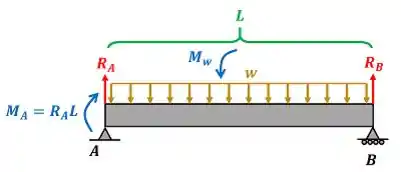
Para usar a equação de equilíbrio de momento da barra e achar , precisamos lembrar que o momento da força distribuída é calculada com a integral abaixo.
Como a força faz a barra tender a girar no sentido horário, vamos colocar um sinal de menos na frente do momento de .
Agora que temos , podemos achar o momento fletor e descobrir o ponto onde ele é máximo através da equação de equilíbrio de momento da parte esquerda da barra no ponto .
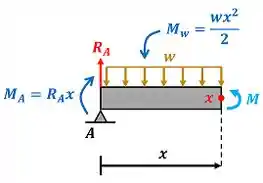
Além disso precisamos lembrar que, como a força faz a barra tender a girar no sentido horário, vamos colocar um sinal de menos na frente do momento de .
Derivando em relação a e igualando a zero, achamos o ponto onde .
Substituindo por na fórmula do momento fletor , achamos .
Passo 3
Agora que temos o momento fletor máximo, podemos achar , substituindo os valores de e na fórmula da tensão máxima , achamos:
Substituindo na equação de , achamos:
No próximo passo acharemos !
Passo 4
Para achar , substituímos a equação do momento fletor que achamos antes na integral de .
Colocando as constantes para fora da integral, achamos:
Substituindo os limites de integração:
Passo 5
Agora vamos dividir por !
Para achar o valor exato dessa divisão, precisamos lembrar que o momento de inércia de uma área retangular vale:
Substituindo isso na fórmula, achamos:
No entanto, o produto é justamente o volume da viga! Substituindo por , achamos:
Reorganizando essa equação:
Aeeeee! É justamente isso que a gente queria demonstrar! Então acabamos com a questão!
Resposta
Ei, a resposta está no passo a passo :)