Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 66
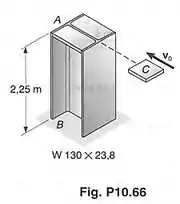
Um bloco de move-se horizontalmente com uma velocidade até chocar-se com a coluna , como mostrado. Usando , determinar a maior velocidade , para que a tensão normal máxima na coluna não exceda a .
Passo 1
Oi, galera! Tudo bem? Vamos fazer uma questão de carregamento produzido por impacto? Você vai ver que consegue mandar muito em resistência dos materiais! Então bora!
A questão quer saber qual é a máxima velocidade do bloco que faz a barra se deformar sem ultrapassar a tensão máxima . A figura abaixo mostra os dados.
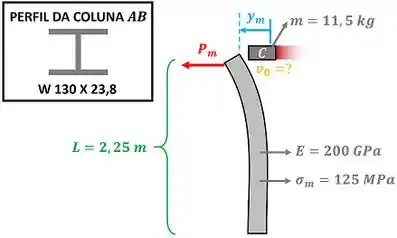
é a máxima força que o bloco faz na coluna sem que ela se deforme permanentemente. é a deformação que o choque do bloco causa e é a massa do bloco.
A velocidade máxima do bloco é uma velocidade que produz a máxima energia cinética que a coluna é capaz de absorver.
No entanto, para calcular precisamos achar a máxima energia que a coluna é capaz de absorver. Calculamos esse valor através de uma equação que relaciona a deformação e a força à energia .
onde será calculado através do diagrama de corpo livre da barra e será obtido usando uma equação de deflexão do apêndice .
Passo 2
Vamos começar os cálculos determinando quanto vale . No entanto, para usarmos o diagrama de corpo livre, temos que determinar primeiro o valor do momento máximo que a coluna suporta. Para isso, vamos utilizar a equação de tensão máxima normal de uma barra em flexão.
onde é o momento de inércia do perfil da barra e é distância entre o centro da barra e o ponto de maior tensão da barra. e são obtidos através das informações do apêndice para um perfil W 130 X 23,8.
Antes de substituir os dados nas fórmulas temos que converter de pra , de pra e de pra . Fazemos isso, multiplicando por , por e por .
Agora sim podemos achar o valor de através do diagrama de corpo livre da barra.
Faremos isso no próximo passo!
Passo 3
Nesse diagrama, vemos que o momento máximo é o momento que a barra sofre no seu engastamento. faremos o equilíbrio de momento da barra no ponto que é o ponto onde a coluna está engastada.
Como consideramos na figura que o momento faz a coluna girar em um sentido horário em torno do ponto , esse momento ganha um sinal de menos na frente.
O equilíbrio de momentos diz que a soma dos momentos é zero. Logo:
Substituindo os valores de e , achamos .
Agora podemos achar e !
Passo 4
Para calcular a máxima deflexão da coluna, usaremos a equação do apêndice de flecha máxima para o primeiro tipo de viga e carregamento.
Para usar essa equação, temos que nos lembrar de converter o módulo de elasticidade de para , multiplicando por .
Substituindo e na equação de , achamos.
Passo 5
Agora sim somos capazes de achar a velocidade máxima do bloco, substituindo na equação de .
Boooooaaaaa! Missão cumprida! Achamos o que a questão pede!