Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 38
Levando em conta somente o efeito das tensões normais, determinar a energia de deformação da viga prismática para o carregamento mostrado.
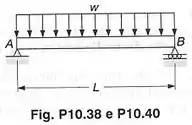
Passo 1
Faaaaala, galerinha! Como estão os estudos? Tem que aprender rápido? Então partiu resolver um exercício de energia de deformação passo a passo e de forma clara!
Nesse exercício precisamos calcular a energia de deformação da barra . Mas atenção! Vamos calcular apenas a energia de deformação da barra que é causada pelo momento fletor presente na barra. Deixaremos a força cortante de fora.
A equação que calcula essa energia da barra causada pelo momento fletor é:
onde é o comprimento total da barra , é o módulo de elasticidade e é o momento de inércia.
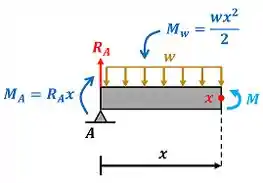
Para calcular o momento fletor , temos que achar as forças que atuam na barra. A figura abaixo mostra as forças atuando na barra .
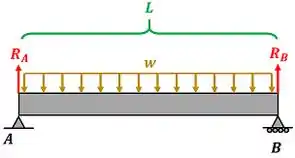
é a força de reação causada pela restrição no ponto e é a força de reação causada pela restrição no ponto . Elas são encontradas através das equações de equilíbrio de momento. No entanto, apenas uma delas é suficiente para a gente achar o momento fletor . No próximo passo, calcularemos uma das duas forças então!
Passo 2
Como vamos calcular o momento fletor fazendo o equilíbrio da parte esquerda da barra, temos que conhecer apenas ! Podemos excluir , porque essa força não vai fazer parte do equilíbrio da parte esquerda da barra!
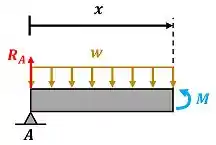
Para achar sem precisar achar , podemos calcular através da equação de equilíbrio de momento no ponto . Como a força não tem braço de alavanca em , ela não aparece na equação de equilíbrio de momento em .
Para usar a equação de equilíbrio de momento da barra e achar , precisamos lembrar que o momento da força distribuída é calculada com a integral abaixo.
Como a força faz a barra tender a girar no sentido horário, vamos colocar um sinal de menos na frente do momento de .
Agora estamos aptos a achar !
Passo 3
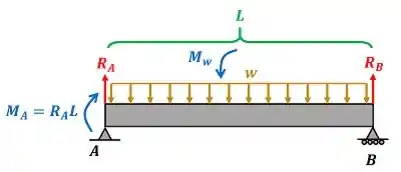
Para achar precisamos usar a equação de equilíbrio de momento da parte esquerda da barra . Calcularemos o equilíbrio de momento no ponto .
Para usar a equação de equilíbrio de momento da parte esquerda da barra e achar , precisamos lembrar que o momento da força distribuída é calculada com a integral abaixo.
Novamente precisamos lembrar que, como a força faz a barra tender a girar no sentido horário, vamos colocar um sinal de menos na frente do momento de .
Com esse valor de , podemos achar !
Passo 4
Agora podemos substituir na integral que calcula .
Colocando as constantes para fora da integral, achamos:
Substituindo os limites de integração:
Uhuuuuuuuul! Boaaaa! Com esse valor de , concluímos mais um exercício de energia de deformação!