Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 55b
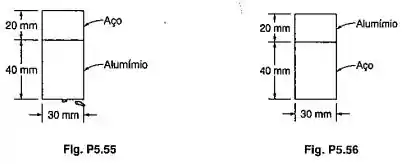
Uma barra de aço ( e uma de alumínio () são firmemente unidas para formar a viga composta mostrada. Para uma força cortante vertical de , determinar (a) a tensão média na superfície de contatos; (b) a máxima tensão de cisalhamento na viga. (Sugestão: Usar o método indicado Prob. 5.52)
Passo 1
No item (a) a gente calculou quase tudo.
Agora precisamos descobrir o momento máximo.
Para isso, vamos começar calculando o momento estático no centroide.
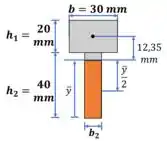
Passo 2
Agora vamos calcular a tensão sobre o centroide. Não se esqueça, na hora de selecionar a espessura devemos utilizar a seção original:
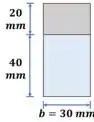
E pra finalizar a questão, é só calcular a tensão. Como não usamos a seção transformada, então deve ser usado
Resposta
Exercícios de Livros Relacionados
Determinar a localização do centro de cisalhamento O de uma viga de parede fina de espessura uniforme e com a seção transversal mostrada.
Determinar a localização do centro de cisalhamento O de uma viga de parede fina de espessura uniforme e com a seção transversal mostrada.
Determinar a localização do centro de cisalhamento O de uma viga de parede fina de espessura uniforme e com a seção transversal mostrada.
A viga em balanço mostrada consiste em um perfil em forma de “Z”, de espessura uniforme. Para o carregamento mostrado, determinar a distribuição de tensões de cisalhamento na perna vertical DE. Os eix
A viga em balanço mostrada consiste em um perfil em forma de “Z”, de espessura uniforme. Para o carregamento mostrado, determinar a distribuição de tensões de cisalhamento na perna vertical DE. Os eix