Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 52
Para uma viga feita de dois ou mais materiais com diferentes módulos de elasticidade, mostra que a Eq. 510
Permanece válida, desde que os valores de e sejam calculados usando a seção transformada da viga (veja Sec 4.7) e desde a espessura seja a largura real da viga, no ponto onde a tensão é calculada
Passo 1
Pra começar, vamos imaginar uma viga com dois materiais.
Pra facilitar, vamos pensar em uma viga quadrada, com dois materiais com módulos de elasticidade diferentes:
O que vamos fazer é transformar essa seção! Pra isso a gente precisa de um módulo de referência . E vamos calcular duas constantes e . Essas constantes representam a divisão dos módulos de elasticidades pelo módulo de referência:
E com isso, a gente transforma as seções. Lembre-se, pra transformar uma seção, basta multiplicar a largura de cada região da viga pelos valores de
Passo 2
Agora temos uma seção transformada:
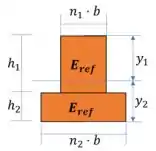
Essa seção transformada terá um momento de inércia , e as distâncias e são em relação ao centroide da seção transversal.
Imagine que a nossa viga está sofrendo um momento qualquer . A tensão em um ponto qualquer será:
Onde o valor de pode ser ou
Passo 3
Show!
Com o valor calculado das tensões podemos calcular o esforço horizontal sobre a viga:
Perceba que a integral representa o momento estático de uma seção! Então a expressão representa o momento estático da seção transformada :
Passo 4
O pior já passou. Agora vamos usar a força para calcular o momento estático:
Quando dividimos um momento por uma distância, encontramos uma força! Neste caso, ao dividir o resultado é a força de cisalhamento
Logo:
E com isso demonstramos a questão!
Resposta
Ei, a resposta está no passo a passo :)