Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 58

A alavanca AB tem uma seção retangular de 10x30 mm. Sabendo-se que θ = 40 º , determinar as tensões, normal e de cisalhamento nos três pontos indicados.

Passo 1

Pra começar, vamos fazer uma seção na região de interesse, e calcular os esforços internos:

N = F ⋅ cos ⁡ θ = 1780   N ⋅ cos ⁡ 40 º = 1363,56   N

V = F ⋅ s en ⁡ θ = 1780   N ⋅ sen ⁡ 40 º = 1 144,1 6   N

M = 1780 ⋅ sen ⁡ 40 º ⋅ 100   m m = 114416   N ⋅ m m

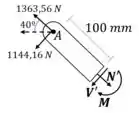
Passo 2

Agora vamos calcular o momento de inércia da seção:

I = b h 3 12 = 10 ⋅ 30 3 12 = 22500   m m 4

E a área da seção transversal:

A = b h = 10 ⋅ 30 = 300   m m 2

E o momento estático no ponto b :

Q = 15 ⋅ 10 ⋅ 15 2 = 1125   m m 3

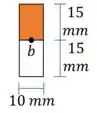
Passo 3

Prontinho. Agora já temos tudo pronto para calcular as tensões.

No ponto a , o cisalhamento é nulo, mas temos tensão normal gerada pela força e pelo momento. Perceba que o momento gera uma tração.

σ a = P A + M c I = 1363,56   N 300   m m 2 + 114416   N   m m ⋅ 15   m m 22500   m m 4 = 80,82   M P a

No ponto b :

σ b = P A = 1363,56   N 300   m m 2 = 4,55   M P a

τ b = V Q I t = 1144,16   N ⋅ 1125   m m 3 22500   m m 4 ⋅ 10   m m = 5,72   M P a

No ponto c o momento gera uma compressão:

σ c = P A - M c I = 1363,56   N 300   m m 2 - 114416   N   m m ⋅ 15   m m 22500   m m 4 = - 71,73   M P a

Resposta

σ a = 80,82   M P a

σ b = 4,55   M P a

τ b = 5,72   M P a

σ c = - 71,73   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determinar a maior tensão de cisalhamento, na seção n - n .
Determinar a maior tensão de cisalhamento na seção n - n .
Para a viga em balanço e o carregamento dado, determinar o ponto onde a tensão de cisalhamento é mázima e o corresponde valor da tensão: (b) ao longo da linha D ' E ' de uma perna.
Determinar a localização do centro de cisalhamento O de uma viga de parede fina de espessura uniforme e com a seção transversal mostrada.
Uma viga de parede fina com espessura uniforme tem a seção transversal mostrada. Determinar a dimensão b , para que o centro de cisalhamento da viga esteja localizado no ponto indicado.