Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 89
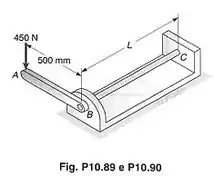
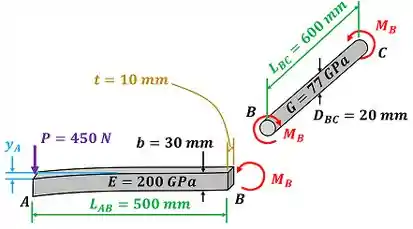
A barra de aço , de diâmetro , é presa à alavanca e ao apoio fixo . A alavanca uniforme de aço tem de espessura e de largura. Usando o método do trabalho e energia, determinar a deflexão do ponto , quando . Usar e .
Passo 1
Oi, galera! Como estão? Bora resolver uma questão de cálculo de deflexão através do método de energia pra mandar muito bem na prova?
Essa questão mostra uma alavanca sendo carregada com uma força . Essa força faz a alavanca sofrer flexão com um momento fletor e a barra sofrer torção com um torque . Por causa disso, a alavanca e a barra absorvem uma energia total e se deformam. O enunciado pede que a gente ache a deflexão da extremidade da alavanca.
O enunciado quer que a gente calcule através do método de trabalho e energia. Isso quer dizer que achamos , usando duas equações para calcular a energia total que e absorvem. A primeira equação, calcula a partir da força . Dessa forma, conseguimos deduzir uma equação para .
A segunda equação, calcula , somando a energia absorvida pelo eixo com a energia absorvida pela alavanca .
Para calcular usamos a equação do exemplo 10.3 do livro que calcula justamente a energia de uma barra que sofre flexão por conta de uma força .
é obtida usando a equação 10.22 do livro que calcula a energia absorvida por um eixo em torção.
Agora que temos todas essas fórmulas, vamos começar a fazer as contas, calculando o valor do momento de inércia da alavanca e do momento polar da barra .
Passo 2
Achamos através da fórmula de momento de inércia polar para áreas circulares abaixo. Antes, devemos converter o diâmetro de pra , multiplicando eles por .
Encontramos através da fórmula do momento de inércia para áreas quadrangulares abaixo. Antes, devemos converter a largura e a espessura de pra , multiplicando eles por .
Agora temos que achar o momento para conseguir encontrar !
Passo 3
Calculamos o momento , fazendo o equilíbrio de momentos da alavanca no ponto . O equilíbrio de momento diz que a soma dos momentos e (momento da força ) deve valer zero. Logo:
No entanto, é a força multiplicada pelo braço de alavanca que vale se convertermos seu valor de pra .
Substituímos os dados nas equações de e para achar as energias de deformação. No entanto, antes disso converter o e o de para , multiplicando e por .
Somando com , achamos .
Substituindo esse valor na fórmula de , achamos:
Aeeeeee! Chegamos no final da questão! Parabéns pra gente!