Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 56

A barra de aço AB tem uma seção transversal quadrada de 10 × 10 m m ,   e é mantida por pinos que estão separados por uma distância fixa de 0,2 m , e afastados de e = 0,9   m m do eixo geométrico da barra. Sabendo-se que na temperatura T 0 os pinos estão em contato com a barra, e que a força na barra é zero, determinar o aumento de temperatura para que a barra estabeleça o contato com o ponto C, se d=0,3mm. Usar E = 200   G P a e o coeficiente de dilatação térmica 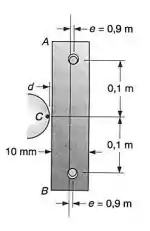α = 11,7 × 10 - 6 ° C .

Passo 1

E ai galera tudo bem? O enunciado pede que a gente determine o aumento de temperatura para que a barra estabeleça o contato com o ponto C, começaremos determinando a informações necessárias como a área, inércia , pressão, vem comigo :D

A = 3 8 3 8 = 0,140625   i n 2

I = 1 12 3 8 4 = 1,64795 × 10 - 3 i n 4

E I = 29 × 10 6 1,64795 × 10 3 - 47791 l b ∙ i n 2

P c r = π 2 E I L 2 = π 2 47791 8 2 = 7370   l b .

Passo 2

Calcule P usando a fórmula da secante

y m a x = d = e s e c s e c   π 2 P P c r   - 1   s e c s e c     π 2 P P c r   = 1 + d e

π 2 P P c r = 1 + d e - 1   = 1 + 0,01 0,03 - 1   = 0,75 = 0,72273  

P P c r = 2 π 0,72273 2 = 0,21170     P = 0,21170 P c r = 1560,2   l b .

Passo 3

Análise Termal

  1. Aproximação simples ignorando a excentricidade

    2. Alongamento total = α L Δ T - P L E A = 0

    Δ T = P L E A 1 α L = P E A α = 1560,2 29,10 6 0,140625 6,5 × 10 - 6 = 58,9 ° F

  2. Análise com inclusão da excentricidade.

Alongamento total do eixo centroide = α L Δ T - P L E A = 2 e d y d x | x = 0

Para calcular d y d x , diferencie e q .   10.26

d y d x = e ( p t a n t a n   P L 2   c o s c o s   p x   - p s i n s i n   p x )  

Passo 4

Em x = 0               d y d x | x = 0 = e p t a n t a n   P L 2   = e P E I t a n t a n   π 2 P P c r  

O alongamento do eixo centroide é 2 e 2 P E I t a n t a n   π 2 P P c r    

= 2 0,03 2 1560,2 47791 t a n t a n   0,72273   = 286,8 × 10 - 6 i n .

α L Δ T = P L E A + 2 e d y d x | x = 0

Δ T = P E A α + 286,8 × 10 - 6 α L = 58,9 + 286,8 × 10 - 6 6,5 × 10 - 6 8 = 58,9 + 5,5 ° = 64,4 ° F

Resposta

64,4 ° F

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Verifique se a coluna de madeira é adequada para suportar a carga excêntrica P = 3 kN aplicada no topo. Ela está engastada na base e é livre no topo. Use as equações NFPA da Seção 13.6 e a Equação 13.
O poste de utilidades de 250 mm de diâmetro suporta o transformador que pesa 3 kN e tem centro de gravidade em G. Se o poste estiver engastado no solo e livre no topo, determine se ele é adequado de a
Determine a carga excêntrica máxima admissível P que pode ser aplicada à coluna de madeira engastada na base e livre no topo. Use as equações NFPA da Seção 13.6 e Equação 13.30.
Usando as equações NFPA da Seção 13.6 e a Equação 13.30, determine a carga excêntrica máxima admissível P que pode ser aplicada à coluna de madeira. Ela está presa por pino na extremidade e engastada
A coluna de madeira é usada para suportar uma carga axial P=150k N . Se estiver engastada na base e livre no topo, determine a largura mínima da coluna com base nas fórmulas NFPA.