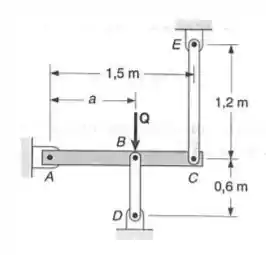
A barra rígida ABC é suportada por duas hastes de ligação BD e CE, de seção transversal retangular uniforme de e é feita de um aço doce, que é assumido ser elastoplástico com e . A intensidade Q de uma força aplicada em B cresce gradualmente desde zero até a deflexão em B atingir e então decresce até zero. Sabendo-se que , determinar:

b) A deflexão residual do ponto B e a tensão residual da barra BD

(nota do expert: o item B apresenta uma falha de elaboração pedindo a deformação total, tendo em vista que já sabemos que a mesma foi de pelo enunciado, assim, o item B foi replanejado com o intuito de da melhor maneira o que o enunciado pede.)

Sabemos que o ponto B deformou ao todo , assim, sabemos que essa deformação possui duas contribuições, uma referente ao regime elástico, ou regime de escoamento, e nesse caso sabemos que a tensão de escoamento vai ser dada por:

Como a nossa barra BD entrou em escoamento, sabemos que a máxima tensão que age nela é dada por:

Além da deformação plástica, sabemos também que a deformação platica vai atuar na nossa viga, assim, podemos definir que a deformação total nela é dada por:

Pelo enunciado nos é dito que a deformação total da nossa barra é dada por:

Sabemos que:

Assim teremos que: