Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 3.Problemas - Ex. 53
A barra uniforme de comprimento gira livremente em torno de um eixo horizontal através de . Se a mola de módulo não é esticada quando é coincidente com A, determine a tensão necessária para segurar a barra na posição de mostrada. O diâmetro da polia pequena em é insignificante.
Passo 1
Fala galera! Tudo certo? Vamos dividir a resolução em algumas etapas, beleza? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar a tensão necessária para segurar a barra inclinada em . Para começar a resolver nosso problema, vamos primeiro fazer o diagrama de corpo livre.
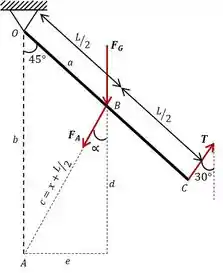
Além das forças acima, temos as reações no ponto que não foram ilustradas, pois faremos o somatório de momentos em torno deste ponto. Por convenção, vamos considerar as forças como positivas quando elas estiverem no sentido positivo dos eixos e os momentos positivos quando estiverem no sentido horário.
Fazendo então o equilíbrio de momentos em torno de , temos:
Passo 2
Tá, mas e agora???
Calma que vai dar certo! Para calcular usando essa expressão, precisamos encontrar e . O comprimento pode ser obtido por semelhança de triângulos e também pode ser relacionado com por , então:
E o ângulo , consequentemente:
Passo 3
Substituindo esses valores de e na equação do momento do Passo 1, temos:
Ufa! Essa já foi hein? Partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 