Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 105
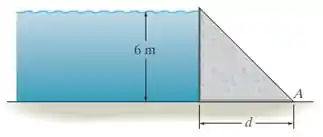
A barragem de concreto por ‘gravidade’ é mantida no lugar por seu próprio peso. Se a densidade do concreto é , e a água tem uma densidade de , determine a menor dimensão que impedirá que a barragem tombe em torno de sua extremidade .
Passo 1
Falaa! Ele quer saber o comprimento para que essa barragem não tombe por causa da pressão da água.
Um cara chamado Pascal enunciou uma vez que, um fluido em repouso cria uma pressão em um ponto que é a mesma em todas as direções. A intensidade de , medida como uma força por área unitária, depende do peso específico ou densidade de massa do fluido e da profundidade do ponto a partir da superfície do fluido. Podemos escrever a expressão da pressão como:
Vamos considerar que a barragem tem metro de largura, beleza? Tendo isso em mente, vamos descobrir a intensidade de carga que a água causa na barragem:
Passo 2
Podemos imaginar que a distribuição de pressão na parede da barragem tem formato triangular. Vale zero na superfície e no fundo. Aí a gente pode calcular a força resultante e a posição dela pelas regrinhas de estática:
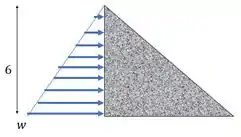
A força resultante da água na barragem pode ser escrita como a área desse triângulo que representa a distribuição
Essa força atua através do centroide dessa área, logo
Passo 3
Nos falta ainda saber o valor do peso da barragem, . Logo, o valor de será escrito da seguinte forma:
Onde é largura da barragem que vamos considerar como 1, é a densidade do concreto, é a gravidade, a profundidade da barragem e quem a gente quer achar.
Substituindo os valores na expressão, temos:
Como a seção é triangular, esse peso vai estar posicionado no centroide do triângulo, em:
Passo 4
Um DCL do que está acontecendo:
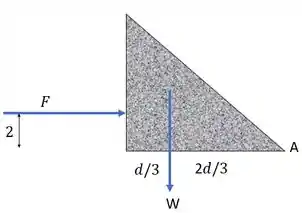
Agora que temos todas as informações de forças atuando na barragem, vamos calcular o momento no ponto , a fim de encontrarmos o valor de . O somatório dos momentos para sistemas em equilíbrio é igual a zero. Assim, adotando como sentido positivo anti-horário, temos:
Resposta
A menor dimensão que impedirá que a barragem tombe é: