Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas - Ex. 50

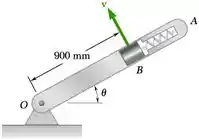
Um bloco B de 250 g se encaixa dentro de uma pequena cavidade aberta no braço OA, que gira no plano vertical a uma taxa constante tal que v = 3 m/s. Sabendo que a mola exerce no bloco B uma força de intensidade P = 1,5 N e desprezando o efeito do atrito, determine o intervalo de valores de θ para os quais o bloco B faz contato com a face da cavidade fechada para o eixo de rotação O.

Passo 1

E aí gurizada tudo certinho? Vamos agora neste exercício ter que determinar o intervalo de valores de θ para os quais o bloco B faz contato com a face da cavidade fechada para o eixo de rotação O. Vamos trazer as equações do livro para cá, okay?

+ ↙ Σ F n = m a n :         P + m g sin ⁡ θ - Q = m v 2 ρ

Para ter contato com a superfície especificada, precisamos Q ≥ 0 ,

Q = P + m g sin ⁡ θ - m v 2 ρ ≥ 0

Isolando seno temos:

sin ⁡ θ ≥ 1 g v 2 ρ - P m

Passo 2

Agora vamos resgatar os dados do enunciado para os cálculos :D

m = 0.250   kg ,         v = 3   m/s ,           P = 1.5   N ,         ρ = 0.9   m

Substituindo em (1)

sin ⁡ θ ≥ 1 9.81 ( 3 ) 2 0.9 - 1.5 0.25

sin ⁡ θ ≥ 0.40775

Resposta

24.1 ° ≤ θ ≤ 155.9 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

133. O caminhão tem massa de 50Mg quando está vazio. Quando está descarregado 5 m 3 de areia a uma taxa constante de 0,8 m 3 s , a areia flui para fora a uma velocidade de 7m/s, medida em relação ao c
138. O vagão é usado para coletar água acumulada em uma calha nos trilhos. Determine a forca necessária para impelir o vagão a uma velocidade constanve v, para cada um dos três casos. O coletor tem um
126. Um limpa-trilhos localizado na frente de uma locomotiva junta neve a uma taxa de 0,27 m 3 / s e a armazena no trem. Se a locomotiva está viajando a uma velocidade constante de 3,6 m/s, determine
127. O barco tem uma massa de 180kg e está viajando por um rio a uma velocidade constante de 70km/h, medida em relação ao rio. O rio está fluindo na direção oposta a 5km/h. Se um tubo é colocado na ág
135. A corrente tem um comprimento total L m ´ . Se uma porção h da corrente é suspensa sobre a mesa e liberada, determine a velocidade de sua extremidade A como função da posição y. Despreze o atrito