Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 55
O bloco A sustenta uma coluna tubular e repousa sobre a cunha B, tal como mostra a figura. O coeficiente de atrito estático em todas as superfícies de contato é 0,25. Se , determine o ângulo para o que o deslizamento seja iminente, a força correspondente exercida no bloco pela parede vertical.
Passo 1
Tá legal! Vamos começar esse excercício desenhando o diagrama de corpo livre para a cunha B:
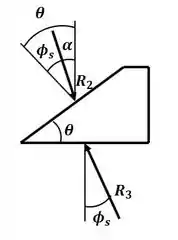
Conforme vimos na seção anterior do livro, o coeficiente de atrito pode ser encontrado através de:
Substituindo o valor dado de :
Passo 2
Agora, analisando o DCL do passo 1, podemos ver que só temos duas forças, dispostas de maneira simétrica em relação à cunha, então, com isso, as forças devem ter mesma magnitude e serem diametralmente opostas, formando também os mesmos ângulos com a vertical, dessa forma:
Então, agora podemos encontrar :
Passo 3
Agora vamos analisar o desenhar o diagrama de corpo livre para o bloco A:
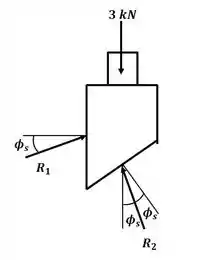
Agora, podemos desenhar o triângulo de forças para o sistema anterior:
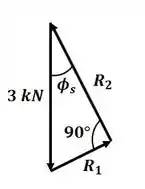
Dessa forma, por trigonometria, podemos encontrar o valor da reação exercida pela parede no bloco: