Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 68

O calço tem um peso insignificante e um coeficiente de atrito estático μ s = 0,35 com todas as superficies de contato. Determine o maior ângulo θ de modo que ele seja ‘autotravante’. Isso requer que não haja de deslizamento para qualquer intensidade de força P aplicada à junta.

Passo 1

O problema pede que descubra o ângulo θ para que o sistema continue travado.

Bom galera, pra facilitar a gente começa fazendo um diagrama de corpo livre para observar melhor.

E a gente faz o diagrama lembrando que o sistema é simétrico e as forças de atrito são calculadas por:

F = μ s N = 0,35 N

O diagrama fica:

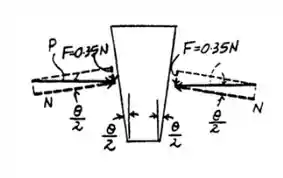
Passo 2

Beleza, agora olha, se a gente reparar bem em um dos lados a gente nota que a força de atrito F pode ser considerado um cateto de um triângulo, e a normal N outro cateto do mesmo triângulo, então dividindo um pelo outro a gente tem uma tangente, assim:

tan ⁡ θ 2 = F N

Passo 3

Agora, tá fácil, é só a gente pegar a força de atrito estática máxima e pegamos o inverso da tangente:

θ 2 = tan - 1 ⁡ θ 2 = 0,35 N N

θ 2 = 19,29 °

θ = 38,58 °

Resposta

θ = 38,58 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O mecanismo de freio consiste em dois braços com pinos e um parafuso de rosca quadrada comroscas esquerda e direita. Assim, quando girado, o parafuso aproxima os dois braços. Se o avanço do parafuso é
Se forças de binário F = 35N forem aplicadas ao punho da morsa, determine a força compressiva desenvolvida no bloco. Desconsidere o atrito no mancal A . A guia em B é lisa. O parafuso de rosca quadrad
Um esticador, semelhante ao mostrado na F i g u r a8.17 , é usado para tracionar o elemento ABda treliça. O coeficiente de atrito estático entre os parafusos com rosca quadrada e o esticador é μ s = 0
Se a força de retenção na placa A tiver de ser 2k N , determine o torque M que deverá ser aplicado ao parafuso para apertá-lo. O parafuso de rosca quadrada tem raio médio de 10m m e avanço de rosca de
Se a força de aperto necessária na placa A tiver de ser 50N , determine o torque M que deveráser aplicado ao punho do grampo “ C ” para apertá-lo contra a placa. O parafuso de rosca quadrada tem raio