Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas fundamentais - Ex. 01

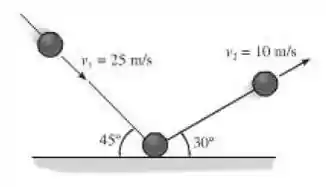
A bola de 0,5 kg atinge o solo áspero e ricocheteia com as velocidades mostradas. Determine a intensidade do impulso que o solo exerce sobre a bola. Suponha que a bola não desliza quando atinge o solo e despreze a dimensão da bola e o impulso produzido pelo peso da bola.

Passo 1

Analisando o comportamento da bola ao quicar sobre o chão, pode-se dividir a análise em duas componentes, uma para o movimento horizontal e outra para o vertical, de tal modo que:

→ +     m v 0 x + ∑ ∫ t 1 t 2 F x d t   =     m v x

+ ↑   m v 0 y + ∑ ∫ t 1 t 2 F y d t   =     m v y

Passo 2

Para o movimento horizontal, teremos que:

→ +     m v 0 x + ∑ ∫ t 1 t 2 F x d t   =     m v x

0,5 * 25 * c o s 45 ° -   ∑ ∫ t 1 t 2 F x d t   = 0,5 * 10 * c o s 30 °

I x =   ∑ ∫ t 1 t 2 F x d t  

8,839 -   I x   = 4,33                           ∴       I x = 4,509   N . s  

Para o movimento vertical, teremos que:

+ ↑   m v 0 y + ∑ ∫ t 1 t 2 F y d t   =     m v y

-   0,5 * 25 * s e n 45 ° +   ∑ ∫ t 1 t 2 F y d t = 0,5 * 10 * s e n 30 °  

I y =   ∑ ∫ t 1 t 2 F y d t  

- 8,839 +   I y   = 2,5                           ∴       I y = 11,339   N . s

Passo 3

Descobertas as componentes do impulso em cada direção, de forma geral para vetores, aplica-se a norma com o objetivo de obtenção do impulso resultante:

I =   I x 2 + I y 2     =     4,509 2 + 11,339 2     ∴                           I = 12,203   N . s

Resposta

A intensidade do impulso atuante na bola para as condições dadas é de 12,203 N.s.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

138. O vagão é usado para coletar água acumulada em uma calha nos trilhos. Determine a forca necessária para impelir o vagão a uma velocidade constanve v, para cada um dos três casos. O coletor tem um
126. Um limpa-trilhos localizado na frente de uma locomotiva junta neve a uma taxa de 0,27 m 3 / s e a armazena no trem. Se a locomotiva está viajando a uma velocidade constante de 3,6 m/s, determine
127. O barco tem uma massa de 180kg e está viajando por um rio a uma velocidade constante de 70km/h, medida em relação ao rio. O rio está fluindo na direção oposta a 5km/h. Se um tubo é colocado na ág
135. A corrente tem um comprimento total L m ´ . Se uma porção h da corrente é suspensa sobre a mesa e liberada, determine a velocidade de sua extremidade A como função da posição y. Despreze o atrito
131. O avião a jato de 12Mg tem uma velocidade constante de 950 km/h ao voar ao longo de uma linha reta horizontal. O ar penetra nas cavidades de entrada de ar S a uma taxa de 50 m 3 s . Se o motor qu