Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 151
Uma bola de que se move a uma velocidade de atinge uma placa de sustentada por molas. Admitindo que não haja perda de energia no impacto, determine a velocidade da bola imediatamente após o impacto, o impulso da força exercida pela placa sobre a bola.
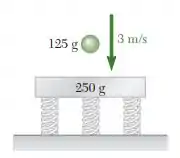
Passo 1
Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão. Para o sistema bola e placa, o momento é conservado, portanto:
Substituindo:
Como não já energia perdida, a energia cinética do sistema é conservada. Logo, antes do impacto temos que ’:
E depois do impacto, temos:
Substituindo :
Lembra que eu te falei sobre a conservação de emergia cinética? Chegou a hora de a utilizarmos. Fica assim:
Substituindo:
Resolvendo esta equação, vamos encontrar que:
Passo 2
Agora para encontramos o impulso, podemos utilizar a seguinte relação:
Que nos diz que a quantidade de movimento linear de uma partícula no instante pode ser obtida adicionando-se à sua quantidade de movimento no instante e os impulsos das forças exercidas sobre a partícula durante o intervalo de tempo de a . Substituindo:
É isso, galera. Bora zerar esse livro!