Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 39
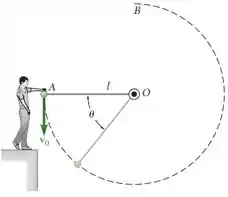
A esfera em é empurrada para baixo com velocidade e oscila em um círculo vertical de raio e centro . Determine a menor velocidade para que a esfera atinja o ponto oscilando em torno do ponto (a) se for uma corda, (b) se for uma barra delgada de massa desprezível.
Passo 1
Vamos lá! Como estamos em um capítulo que trabalha com trabalho e energia, vamos utilizar esta metodologia para resolver esta questão!
O fato de ser uma corda ou uma barra afetará apenas no final da questão. Portanto, o desenvolvimento da nossa questão será o mesmo para ambas as letras.
Aqui temos uma aplicação direta do princípio do trabalho e energia. No ponto inicial, a esfera possui uma velocidade . Já no ponto final, ela terá velocidade (que nada sabemos ainda). Portanto, as energias cinéticas são:
E como a única força a qual a esfera está submetida é a força peso, o trabalho desta força sobre a esfera será:
Portanto, pelo princípio de trabalho e energia, temos:
Passo 2
Até o final do Passo 1 nós não precisamos nos preocupar com o fato de ser uma corda ou uma barra.
Mas agora não mais, temos que separar a nossa análise. Sendo assim, vamos começar identificando a menor velocidade para o caso em que é uma corda.
Para que a velocidade seja mínima, a tensão na corda no ponto deve ser nula (caso contrário, a força centrípeta deverá ser maior, e consequentemente, a velocidade). Portanto, no ponto , a força centrípeta deve ser igual a força peso. Logo,
Portanto, a velocidade mínima será:
Passo 3
Para a letra b), no caso em que é uma barra rígida, não precisamos nos preocupar com a tensão na barra, pois ela será capaz de suportar o peso.
Desta forma, a velocidade final da esfera pode ser igual a 0. Logo, a mínima velocidade é: