Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 4.Problemas - Ex. 79
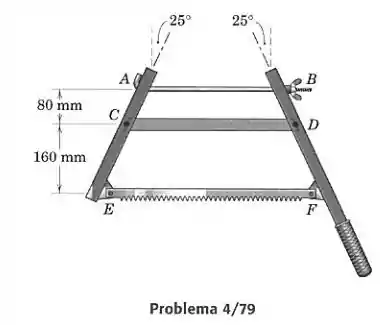
A borboleta da serra dobrável é apertada até que a tração na barra valha 200 N. Determine a força na lâmina de serra e o módulo da força suportada pelo pino .
Passo 1
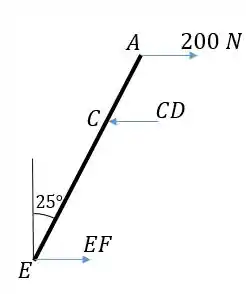
Se isolarmos a barra , vemos que ela está sujeita à força horizontal de 200 N e às forças também horizontais e :
Passo 2
Encontramos diretamente fazendo o momento em torno do pino ser zero:
Como o valor deu positivo, a força está tracionando a barra , como desenhamos.
Passo 3
Agora que temos 2 forças conhecidas e uma desconhecida, podemos fazer o equilíbrio das forças horizontais para encontrar :
Como :
Como a força na barra é de 300 N, a reação em será de 300 N.
Resposta
Exercícios de Livros Relacionados
A chave A é usada para segurar o tubo em uma posição estacionária enquanto a chave B é usadapara apertar a conexão em joelho. Determine a intensidade da força F B a fim de desenvolver um momento de 50
A porca na roda do automóvel deverá ser removida usando a chave e aplicando a força verticalde F=30N em A . Determine se essa força é adequada, sabendo que é necessário um torque inicial de 14N ⋅ m em
Resolva o Problema 4.60 se o tubo de alongamento AB for encaixado no braço da chave e a força de 30N puder ser aplicada em qualquer ponto e em qualquer direção nesse conjunto.
Determine a intensidade do momento da força F = 50 i - 20 j - 80 kN em relação à linha de base C A do tripé.
Determine o momento da força F em relação ao ponto O. Expresse o resultado como um vetor cartesiano.