Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 4.Problemas - Ex. 104
O estrado da empilhadeira da máquina do Prob 4/98 está mostrado com detalhes dimensionais adicionais. Determine a força no cilindro hidráulico único, . A massa do cubo de tijolos é de 2000 kg, com centro de massa em . Você pode desprezar os efeitos da massa dos componentes do estrado.
Passo 1
Vamos isolar nosso corpo de interesse em um diagrama de corpo livre, mostrando as 3 forças que atuam nele:
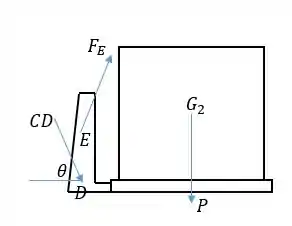
Passo 2
Vamos conseguir diretamente através da equação de momento em relação ao ponto . Precisamos primeiro do ângulo que faz com a horizontal, e pra isso usamos as distâncias horizontal e vertical de até dadas no enunciado:
Agora fazemos o momento em torno de ser zero. Devemos prestar atenção que cada componente de causa um momento anti-horário (positivo):
Resposta
Exercícios de Livros Relacionados
47. A força F → = 6 i + 8 j + 10 kN cria um momento em relação ao ponto O de M 0 = - 14 i + 8 j + 2 kN ⋅ m . Se a força passa por um ponto tendo uma coordenada x de 1m , determine as coordenadas y e z
53. A ferramenta é usada para fechar válvulas de gás que são difíceis de acessar. Se a força F → é aplicada no cabo, determine a componente do momento criada em relação ao eixo z da válvula.
60. Determine a intensidade do momento produzido pela força F = 200N em relação ao eixo da dobradiça (o eixo x) da porta.
55. Determine o momento da força F → em relação ao eixo que se estende entre A e C. Expresse o resultado como um vetor cartesiano.
58. Se F = 450N , determine a intensidade do momento produzido por essa força sobre o eixo x.