O cabo uniforme pesando é mantido na posição mostrada na figura por uma força horizontal aplicada em . Sabendo que e , determine (a) a localização do ponto , (b) O comprimento do cabo.
Passo 1
Bom galera, vamos fazer um diagraminha de corpo livre, só pra facilitar nossa vida:
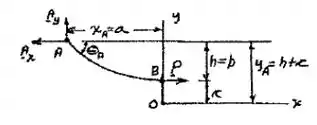
Com isso, de cara a gente já tem alguns valores:
Passo 2
Show de bola, agora em , a gente tem que a tensão máxima é:
Também, tem a equação :
Logo:
Passo 3
Calma, tá quase acabando. Vamos usar agora a equação :
Resolvendo a equação, a gente encontra:
Passo 4
Por fim, a gente usa a equação para encontrar que é a o comprimento: