Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 140

Um motor M é usado para lentamente o cabo mostrado na figura. Sabendo que a massa por unidade de comprometimento do cabo é 0,4   k g / m , determine a tração máxima no cabo quando h = 3   m .

Passo 1

Bom galera, vamos fazer um diagraminha de corpo livre, só pra facilitar nossa vida:

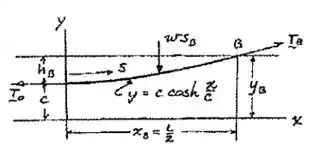
Com isso, de cara a gente já tem alguns valores:

w = 0,4   k g / m

L = 10   m

h B = 3   m

Passo 2

Show de bola, agora a gente pode usar a equação 7.16 :

y B = c cosh ⁡ x B c

→ h B + c = c cosh ⁡ L 2 c

→ 3 + c = c cosh ⁡ 10 2 c

Resolvendo isso a gente pode encontrar:

c = 4,5945   m

Passo 3

Calma, tá quase acabando. Vamos calcular y B :

y B = h B + c

→ y B = 3 + 4,5945

→ y B = 7 , 5945   m

E com isso, temos também a tensão máxima, que é:

T m = T B = w y B

→ T m = 0,4 ⋅ 9,81 7,5945

→ T m = 29,8   N

Resposta

T m = 29,8   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

71- Usando o método da Seção 7.6 , resolva o Problema 7.39 .
72- Usando o método da Seção 7.6 , resolva o Problema 7.40
Para o carregamento na viga determine (a) os diagramas de momento fletor e cortante e (b) os valores absolutos máximos de momento fletor e esforço cortante.
Se a = 0,3 e a reação é uniformemente distribuída no solo, determine (a) os diagramas de cortante e momento fletor e (b) os valores máximos absolutos de momento e cortante.
Para o carregamento na viga determine (a) os diagramas de momento fletor e cortante e (b) os valores absolutos máximos de momento fletor e esforço cortante.